A Comprehensive Guide to Molecular Dynamics Simulation: From Foundational Protocols to Advanced Applications in Drug Discovery

Abstract

This article provides a comprehensive guide to molecular dynamics (MD) simulation protocols, tailored for researchers, scientists, and professionals in drug development. It covers the foundational principles of MD, including system setup, force field selection, and integration algorithms. The guide then explores advanced methodological applications across biomedical fields, from studying protein-ligand interactions for virtual screening to modeling complex systems like lipid nanoparticles. It addresses common troubleshooting and optimization challenges, offering solutions for sampling efficiency and force field accuracy. Finally, the article details rigorous validation techniques against experimental data and comparative analyses of different MD approaches, emphasizing the growing integration of machine learning to enhance simulation power and accuracy.

Understanding the Core Principles: A Beginner's Guide to MD Simulation Setup

Molecular Dynamics (MD) simulation is a computational technique that predicts the time-dependent behavior of every atom in a molecular system, such as a protein surrounded by water or a lipid bilayer [1]. The core of this method relies on a molecular mechanics force field—a mathematical model that describes the potential energy of a system as a function of its atomic coordinates. The force field is used to calculate the forces acting on each atom, which are then used to propagate the system forward in time according to Newton's laws of motion [2] [1]. The accuracy and reliability of an MD simulation are fundamentally dependent on the quality of the force field employed. This application note details the essential components of a classical force field, provides protocols for its application in biomolecular simulations, and presents a structured overview of current force field types and parameterization strategies.

Core Components of a Classical Force Field

A force field is a collection of parametric equations and corresponding parameter sets used to calculate the potential energy of a system of atoms [2] [3]. The total potential energy ((E{total})) in an additive force field is typically decomposed into bonded and non-bonded interactions: (E{total} = E{bonded} + E{non-bonded}) [2] [4].

Table 1: Core Energy Terms in a Biomolecular Force Field

Energy Term	Mathematical Form	Physical Description	Key Parameters
Bond Stretching	(E{bond} = \frac{k{ij}}{2}(l{ij}-l{0,ij})^2) [2] [4]	Energy change as a covalent bond stretches/compresses from its equilibrium length.	Force constant (k{ij}), equilibrium bond length (l{0,ij}).
Angle Bending	(E{angle} = k{\theta}(\theta{ijk}-\theta0)^2) [4]	Energy change as the angle between two adjacent bonds deviates from equilibrium.	Force constant (k{\theta}), equilibrium angle (\theta0).
Torsional Dihedral	(E{dihed} = k\phi(1 + \cos(n\phi - \delta))) [2] [4]	Energy barrier for rotation around a central bond, defined for four sequentially bonded atoms.	Force constant (k_\phi), periodicity (n), phase angle (\delta).
Improper Dihedral	(E{improper} = k\phi(\phi - \phi_0)^2) [4]	Harmonic potential used to enforce planarity (e.g., in aromatic rings or conjugated systems).	Force constant (k\phi), equilibrium angle (\phi0).
van der Waals (Non-bonded)	(V_{LJ}(r) = 4\epsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6} \right]) [2] [4]	Lennard-Jones potential describing short-range Pauli repulsion ((r^{-12})) and London dispersion attraction ((r^{-6})).	Well depth (\epsilon), van der Waals radius (\sigma).
Electrostatics (Non-bonded)	(E{Coulomb} = \frac{1}{4\pi\varepsilon0} \frac{qi qj}{r_{ij}}) [2] [4]	Coulombic interaction between fixed partial atomic charges.	Atomic partial charges (qi, qj).

The following diagram illustrates the logical workflow of how a force field calculates the total potential energy of a molecular system by summing these individual components.

Diagram 1: Hierarchy of potential energy terms in a classical force field. The total energy is a sum of bonded and non-bonded components, each comprising several specific interaction types.

Advanced Considerations: Force Field Types and Polarizability

Classical force fields can be systematically classified based on their level of detail and treatment of electronic effects, particularly polarization [5] [4] [3].

Table 2: Classification of Molecular Force Fields

Classification	Description	Common Examples
Class 1 (Additive)	Uses harmonic potentials for bonds/angles and fixed atomic charges. Computationally efficient but neglects polarization [4].	AMBER, CHARMM, GROMOS, OPLS-AA [5] [4] [3].
Class 2 (Anharmonic)	Adds cubic/quartic terms and cross-coupling terms for more accurate vibrational spectra [4].	MMFF94, UFF [4].
Class 3 (Polarizable)	Explicitly includes electronic polarization, where the charge distribution responds to the local electric field, improving accuracy [5] [4].	AMOEBA (induced dipoles), CHARMM-Drude (Drude oscillators) [5] [4].
Coarse-Grained	Represents multiple heavy atoms as a single interaction center, sacrificing chemical detail for simulation speed and access to larger time/length scales [2] [3].	Martini (4-to-1 mapping) [6].

Successful setup of an MD simulation requires several key "research reagents"—software tools, force fields, and parameter sets.

Table 3: Essential Research Reagent Solutions for MD Simulations

Reagent / Resource	Function / Description	Example Uses
Biomolecular Force Fields	Pre-parameterized sets of equations and parameters for simulating proteins, nucleic acids, lipids, and small molecules.	CHARMM36, Amber ff19SB, OPLS-AA/OPLS4 for modeling biomolecules and their interactions [5] [7] [3].
Small Molecule Force Fields	Transferable force fields designed for drug-like molecules and organic compounds.	GAFF, OpenFF, ByteFF, CGenFF for parameterizing ligands, co-factors, and other small molecules [8] [3].
Simulation Software Packages	Software engines that perform the numerical integration of the equations of motion.	GROMACS, NAMD, AMBER, OpenMM, CHARMM for running production MD simulations [5] [9] [1].
Parameterization Tools	Tools that automatically assign force field parameters (atom types, charges, bonds, etc.) to novel molecules.	SwissParam, Antechamber, CGenFF program, MATCH, Force Field Builder [9] [8].
Solvent Models	Pre-defined models for water and other solvents, which are critical for creating a physiological environment.	TIP3P, TIP4P, SPC (rigid); SWM4-NDP (polarizable) for solvating biomolecules [5] [9].

Experimental Protocol: Implementing a Force Field in an MD Simulation

This protocol outlines the steps for setting up and running an MD simulation for a protein-ligand complex, a common scenario in drug development. The example uses the CHARMM force field and the GROMACS simulation package, a widely adopted combination in the research community [9].

System Preparation and Force Field Assignment

• Obtain Initial Coordinates: Acquire a PDB file for the protein and the small molecule ligand.
• Assign Force Field Parameters:
  • Protein: Use the CHARMM36 force field for proteins [5].
  • Ligand/Co-factor: Generate topology and coordinate files for the ligand (e.g., NADPH) and any other small molecules using a parameterization tool like SwissParam [9]. This tool automatically assigns atom types, charges, and bonded parameters compatible with the CHARMM force field.
• Assemble the System: Combine the protein and ligand topologies and coordinates into a single system file.
• Solvation: Solvate the system in a simulation box (e.g., an octahedral box) using an explicit solvent model such as TIP3P water [9].
• Neutralization: Add ions (e.g., Na⁺ or Cl⁻) to replace solvent molecules until the total system charge is neutralized [9].

Energy Minimization and Equilibration

• Energy Minimization: Run an energy minimization using an algorithm like steepest descent to relieve any bad contacts or steric clashes introduced during system setup. Minimize until the maximum force is below a chosen threshold (e.g., 10 kJ/mol) [9].
• System Equilibration - NVT Ensemble: Equilibrate the system with a fixed Number of particles, Volume, and Temperature (NVT) for a short time (e.g., 100-300 ps). Use a thermostat like V-rescale to maintain the target temperature (e.g., 300 K) [9].
• System Equilibration - NPT Ensemble: Further equilibrate the system with a fixed Number of particles, Pressure, and Temperature (NPT) for a short time (e.g., 100-300 ps). Use a barostat to maintain the target pressure (e.g., 1 bar) [9]. This step ensures the system has the correct density.

Production MD and Analysis

• Production Simulation: Run a long, unconstrained production simulation, saving atomic coordinates at regular intervals (e.g., every 1-10 ps) for subsequent analysis.
• Trajectory Analysis: Analyze the saved trajectory using GROMACS tools or other software to calculate properties of interest, such as:
  • Root-mean-square deviation (RMSD) of the protein backbone.
  • Root-mean-square fluctuation (RMSF) of residue positions.
  • Ligand-protein interaction energies and hydrogen bonding patterns.

Emerging Trends and Future Directions

Force field development is a rapidly advancing field. Key trends include the move towards polarizable force fields like Drude and AMOEBA to more accurately model electrostatic interactions [5], and the application of data-driven and machine learning (ML) approaches for parameterization. For instance, the ByteFF force field uses a graph neural network trained on a massive quantum mechanics dataset to predict force field parameters for drug-like molecules, enabling expansive chemical space coverage [8]. Concurrently, efforts are underway to develop standardized, machine-readable data schemes and formats (e.g., TUK-FFDat) for force fields to improve interoperability, reproducibility, and usability across different simulation platforms [3].

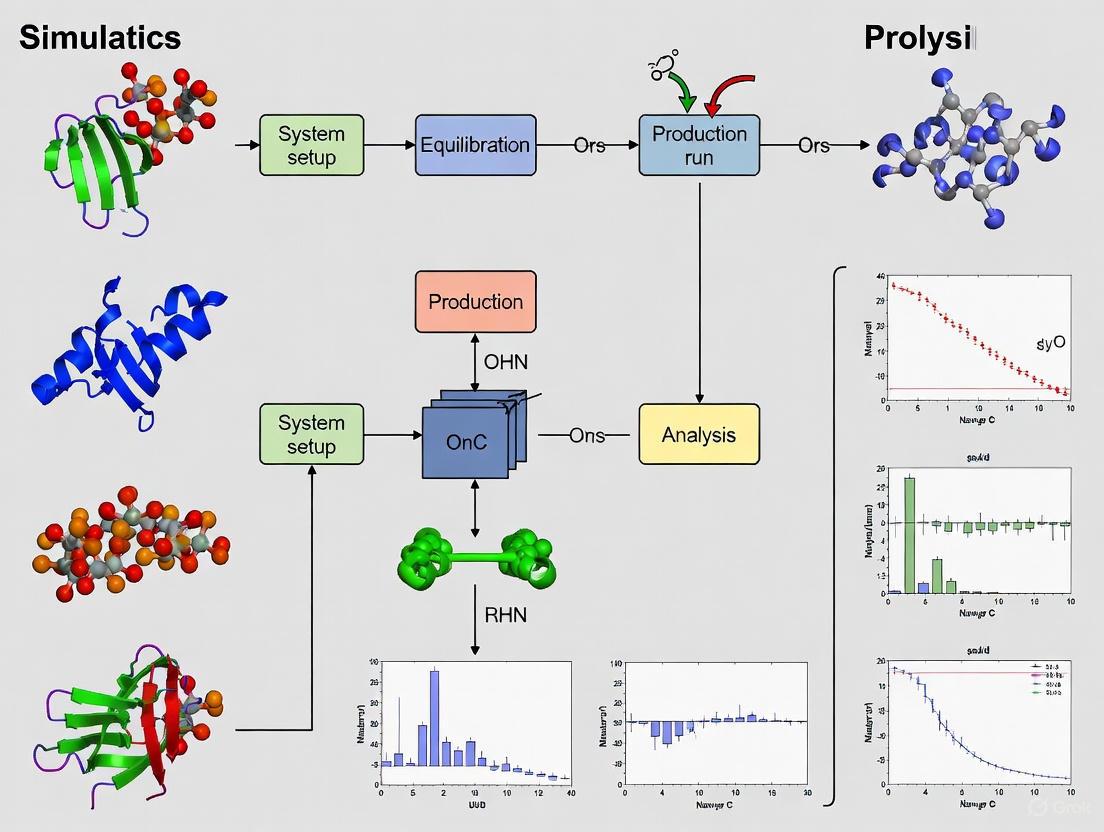
Molecular dynamics (MD) simulation has evolved into a mature technique for understanding the structure-to-function relationships of biological macromolecules by providing insights into their dynamic properties and conformational changes [10]. This protocol details the comprehensive steps required to transition from an initial Protein Data Bank (PDB) file to a production MD run, framed within the broader context of MD simulation protocol research. The procedure addresses critical preparation stages that ensure simulation stability and meaningful results, which is particularly relevant for applications in drug design and the study of biological mechanisms [11] [10]. The workflow encompasses structure validation, system setup, and equilibration phases, each of which is crucial for generating biologically relevant simulation data.

The Scientist's Toolkit: Research Reagent Solutions

Table 1: Essential software tools and their primary functions in MD simulation preparation.

Tool Name	Category	Primary Function
check_structure [11]	Structure Validation	Command-line utility for exhaustive structure quality checking, including alternate conformations and clashes.
VMD [11]	Visualization & Selection	Visual molecular dynamics; structure visualization and atomic selection for PDB file manipulation.
GROMACS [10]	MD Engine	Molecular dynamics simulation package; performs energy minimization, equilibration, and production runs.
AMBER [10]	MD Engine	Suite of biomolecular simulation programs; used for simulation with specific force fields.
NAMD [10]	MD Engine	Parallel MD code designed for high-performance simulation of large biomolecular systems.
BioBB [11]	Library	Provides the check_structure utility within its software suite.
16-Methylpentacosanoyl-CoA	16-Methylpentacosanoyl-CoA, MF:C47H86N7O17P3S, MW:1146.2 g/mol	Chemical Reagent
trans,cis,cis-2,11,14-Eicosatrienoyl-CoA	trans,cis,cis-2,11,14-Eicosatrienoyl-CoA, MF:C41H68N7O17P3S, MW:1056.0 g/mol	Chemical Reagent

Step-by-Step Experimental Protocol

Stage 1: Initial Structure Checking and Preparation

Principle: The foundation of a successful MD simulation is an error-free initial structure. Small errors in the input PDB file can cause simulations to become unstable or yield unrealistic results [11]. This first stage involves a thorough inspection and cleaning of the initial coordinate file.

Methodology:

• Retrieve and Inspect the PDB File: Download your target structure from the Protein Data Bank. Initially, use simple command-line tools to get an overview. The grep command can identify non-protein atoms: grep "^HETATM" your_structure.pdb | wc -l provides a count of HETATM records, often indicating water, ions, or ligands [11].
• Comprehensive Structure Checking: Use the check_structure utility from the BioBB library for an exhaustive check [11].
  • Installation and Execution:

  • Analysis of Output: The tool will report on critical issues [11]:
    • Presence and count of non-protein molecules (e.g., crystallographic waters, ligands).
    • Alternate conformations for specific residues, showing occupancy levels (e.g., ASP A20 CG A (0.50) B (0.50)).
    • Missing side-chain atoms or fragments.
    • Potential clashes between atoms.
    • Possible disulfide bonds (CYS residues involved in cross-links).
• Remediation and Cleaning:
  • Removing Non-Protein Molecules: To create a protein-only file, use check_structure to remove all ligands [11]:
    Alternative with VMD: Load the structure in VMD, use the atom selection "protein" to select all protein atoms, and write the selection to a new PDB file [11].
  • Handling Alternate Conformations: Residues with multiple conformations (e.g., A and B) must be resolved to a single conformation to prevent topology errors. Using check_structure, you can select specific conformers for specific residues [11]:
    Alternative with VMD: In VMD, use a selection command to choose one conformer and the protein backbone [11].
  • Renaming Disulfide-Bonded Cysteines: For simulation preparation with AMBER, cysteines involved in disulfide bonds must be renamed from "CYS" to "CYX" in the PDB file. The check_structure tool can identify and mark these residues [11]:

Stage 2: System Construction and Energy Minimization

Principle: After obtaining a clean protein structure, it must be solvated in a realistic environment (water box, ions) and have its energy minimized. This process removes any residual steric clashes and relaxes the system to a low-energy state, preparing it for the equilibration phase [10].

Methodology:

• Force Field Selection: Choose an appropriate force field (e.g., AMBER, CHARMM, OPLS-AA) for your biomolecule. Parameters are not always interchangeable, and not all force-fields can represent all molecule types [10].
• System Building:
  • Solvation: Place the protein into a box of explicit solvent molecules (e.g., TIP3P water). The box size should provide sufficient margin (e.g., 1.0-1.2 nm) between the protein and the box edges.
  • Neutralization and Ion Concentration: Add ions (e.g., Na⁺, Cl⁻) to neutralize the system's net charge and to bring the ionic concentration to a physiologically relevant level (e.g., 150 mM).
• Energy Minimization: Run a minimization algorithm (e.g., steepest descent) to relieve any atomic clashes introduced during the solvation and ionization process. This step uses the force-field equations to find a low-energy configuration [10].
  • Force Field Calculation: The potential energy is calculated using molecular mechanics force-fields, which are complex but fast-to-calculate equations representing bonds, angles, dihedrals, and non-bonded interactions (van der Waals and electrostatic) [10].

Stage 3: Equilibration and Production MD

Principle: Before data collection (production run), the system must be gently heated and equilibrated at the target temperature and pressure. This ensures the system is stable and possesses correct thermodynamic properties.

Methodology:

• Equilibration Protocol:
  • Perform a two-step equilibration in the NVT (constant Number of particles, Volume, and Temperature) and NPT (constant Number of particles, Pressure, and Temperature) ensembles.
  • NVT Equilibration: Heat the system to the target temperature (e.g., 310 K) using a weak temperature coupling algorithm over a short duration (e.g., 100 ps). Positional restraints are typically applied to the protein heavy atoms to allow the solvent to relax around the protein.
  • NPT Equilibration: Adjust the system density by applying a pressure coupling algorithm (e.g., Parrinello-Rahman) to reach the target pressure (e.g., 1 bar), again with protein restraints.
• Production Run:
  • Remove all positional restraints on the protein.
  • Launch the final, unrestrained MD simulation. The length of this run depends on the biological process being studied, but modern GPU-assisted systems can routinely simulate systems of ~50,000–100,000 atoms for hundreds of nanoseconds to microseconds [10].
  • Integration of Motion: The simulation progresses by numerically integrating Newton's laws of motion. A time step of 1-2 femtoseconds is typically used, which is shorter than the fastest atomic vibrations to ensure numerical stability [10].

Workflow Visualization and Key Parameters

The following diagram illustrates the logical flow and critical decision points of the complete MD setup protocol.

Table 2: Key parameters and their quantitative values for MD simulation stages.

Simulation Stage	Key Parameter	Typical Value / Range	Purpose
System Building	Solvent Box Margin	1.0 - 1.2 nm	Prevents artificial interactions with periodic images.
	Ionic Strength	150 mM	Mimics physiological conditions.
Energy Minimization	Force Tolerance	100 - 1000 kJ/mol/nm	Convergence criterion for stopping minimization.
Equilibration (NVT/NPT)	Temperature	310 K	Simulates biological body temperature.
	Pressure	1 bar	Simulates standard atmospheric pressure.
	Duration (per step)	50 - 500 ps	Allows system relaxation with restraints.
Production MD	Integration Time Step	1 - 2 fs	Ensures numerical stability of the simulation.
	Simulation Length	ns to μs	Captures the biologically relevant process of interest.

Molecular dynamics (MD) simulations have become indispensable in computational chemistry, biophysics, and materials science, enabling researchers to study the physical movements of atoms and molecules over time. These simulations provide critical insights into dynamical behaviors and molecular interactions at an atomic level, playing a pivotal role in various stages of computational drug discovery. The accuracy and efficiency of MD simulations depend heavily on two fundamental components: the software engine used to perform the calculations and the force field that describes the potential energy surface of the molecular system. This application note provides a comprehensive overview of current MD software tools and force fields, framed within the context of establishing robust molecular dynamics simulation protocols for scientific research and drug development.

MD software packages provide the computational framework for simulating the Newtonian equations of motion for systems ranging from hundreds to millions of particles. While numerous packages exist, they share common algorithmic foundations while differing significantly in their implementation, optimization, and target applications.

Fundamental MD Algorithm

The core molecular dynamics algorithm follows a consistent global workflow across most software implementations, as exemplified by GROMACS [12]:

• Input initial conditions: The simulation requires potential interactions (V) as a function of atom positions, initial positions (r) of all atoms, and initial velocities (v) of all atoms
• Compute forces: Forces on each atom are calculated as F~i~ = -∂V/∂r~i~, summing non-bonded pair forces, bonded interactions, and restraining/external forces
• Update configuration: The movement of atoms is simulated by numerically solving Newton's equations of motion: d²r~i~/dt² = F~i~/m~i~
• Output step: Positions, velocities, energies, temperature, pressure, and other properties are written to output files

This process repeats for the required number of simulation steps, with modern implementations leveraging parallel processing and hardware acceleration to maximize performance.

Figure 1: Core Molecular Dynamics Algorithm Workflow. This fundamental workflow is common across most MD software packages, involving initialization, force calculation, configuration updating, and output generation in a cyclic manner.

Major MD Software Platforms

Several MD software packages have emerged as leaders in the field, each with distinct strengths, optimization strategies, and target applications. The table below provides a comparative overview of key MD software platforms:

Table 1: Comparison of Major Molecular Dynamics Software Platforms

Software	Primary Focus	GPU Support	Parallelization	License	Notable Features
GROMACS	Biomolecules (proteins, lipids, nucleic acids)	CUDA, OpenCL, SYCL	MPI, Thread-MPI	LGPL (≥4.6)	Extremely high performance, optimized kernels, user-friendly [13] [14]
AMBER	Biomolecular systems	Yes	MPI	Proprietary, free open source	Specialized for biomolecules, PMEMD engine, advanced sampling [15]
NAMD	Biomolecular systems	CUDA	MPI	Proprietary, free academic use	Excellent parallel scaling, integrated with VMD visualization [15]
AMS	General materials, catalysis	Yes	MPI, OpenMP	Proprietary	Multi-scale modeling, GUI, workflow tools [16] [17]
LAMMPS	Soft/solid-state materials, coarse-grain	Yes	MPI	GPL	Potentials for diverse materials systems [15]
OpenMM	Custom simulation methods	Yes	Python API	MIT	High flexibility, scriptable, excellent GPU performance [15]
CHARMM	Biomolecular systems	Yes	MPI	Proprietary	Commercial version with GUI (BIOVIA) [15]
Desmond	Drug discovery applications	Yes	MPI	Proprietary, commercial or gratis	High performance, comprehensive GUI [15]

Performance Considerations and Hardware Selection

The computational demands of MD simulations necessitate careful hardware selection to maximize performance and efficiency. Different MD software packages have varying optimization characteristics:

CPU Selection: For molecular dynamics workloads, processor clock speeds often take precedence over core count. While sufficient cores are necessary, the speed at which a CPU can deliver instructions to other system components is crucial. A mid-tier workstation CPU with balanced higher base and boost clock speeds, like the AMD Threadripper PRO 5995WX, often provides better performance than extreme core-count processors for many MD workloads. Dual CPU setups with data center processors like AMD EPYC and Intel Xeon Scalable can be considered for workloads requiring more cores [18].

GPU Acceleration: Graphics Processing Units have become pivotal in accelerating molecular dynamics simulations by offloading computationally intensive tasks from CPUs. NVIDIA's latest offerings provide exceptional performance for MD applications [18]:

• NVIDIA RTX 6000 Ada: 48 GB GDDR6 VRAM, 18,176 CUDA cores - ideal for memory-intensive simulations
• NVIDIA RTX 4090: 24 GB GDDR6X VRAM, 16,384 CUDA cores - excellent price/performance balance
• NVIDIA RTX 5000 Ada: 24 GB GDDR6 VRAM, ~10,752 CUDA cores - capable for standard simulations

Software-Specific GPU Recommendations:

• AMBER: Optimized for NVIDIA GPUs, with RTX 6000 Ada ideal for large-scale simulations and RTX 4090 excellent for smaller systems [18]
• GROMACS: Benefits significantly from high GPU throughput, with RTX 4090 providing excellent performance due to high CUDA core count [18]
• NAMD: Recognized for performance optimization with NVIDIA GPUs, significantly enhancing simulation times [18]

Multi-GPU Configurations: Utilizing multi-GPU systems can dramatically enhance computational efficiency and decrease simulation times for AMBER, GROMACS, and NAMD. Benefits include increased throughput, enhanced scalability, and improved resource utilization [18].

Force Fields for Molecular Dynamics

Force fields are mathematical models that describe the potential energy surface of a molecular system as a function of atomic positions. They represent a critical component in MD simulations, determining the accuracy and reliability of the resulting trajectories and properties.

Force Field Fundamentals

Conventional molecular mechanics force fields describe the molecular potential energy surface by decomposing it into various degrees of freedom [8]:

E~MM~ = E~MM~^bonded^ + E~MM~^non-bonded^

The bonded terms include:

• Bond stretching: E~bond~ = ∑~bonds~ k~r~ (r - r~0~)²
• Angle bending: E~angle~ = ∑~angles~ k~θ~ (θ - θ~0~)²
• Torsional rotations: E~torsion~ = ∑~torsions~ ∑~n~ k~Ï•~ [1 + cos(nÏ• - Ï•~0~)]

The non-bonded terms include:

• Van der Waals interactions (typically Lennard-Jones potential)
• Electrostatic interactions (Coulomb's law)

Force field parameters include bonded parameters (equilibrium values r~0~, θ~0~, and ϕ~0~, and force constants k~r~, k~θ~, k~ϕ~) and non-bonded parameters (van der Waals parameters σ and ε, and partial charges q) [8].

Major Force Field Families

Table 2: Comparison of Major Molecular Mechanics Force Fields

Force Field	Class	Coverage	Parameterization Approach	Compatible Software	Key Applications
AMBER	Traditional MM	Biomolecules	Empirical fitting, manual curation	AMBER, GROMACS, NAMD	Proteins, DNA, RNA, lipids [15]
CHARMM	Traditional MM	Biomolecules	Empirical fitting, QM/MM	CHARMM, NAMD, GROMACS	Biomolecular systems [15]
GAFF	Traditional MM	Drug-like molecules	Automated parameterization	AMBER, GROMACS	Small organic molecules [8]
OPLS	Traditional MM	Organic molecules	Liquid-state properties	GROMACS, LAMMPS	Condensed-phase systems [15]
GROMOS	Traditional MM	Biomolecules	Condensed-phase properties	GROMACS	Biomolecular simulations [15]
OpenFF	Modern MM	Drug-like molecules	SMIRKS-based patterns	OpenMM, other packages	Small molecule drug discovery [8]
ByteFF	Data-driven MM	Expansive chemical space	GNN-predicted parameters	AMBER-compatible	Drug discovery applications [8]
Espaloma	ML-based MM	Small molecules	Graph neural networks	OpenMM	Transferable parameters [8]

Recent Advances in Force Field Development

Traditional look-up table approaches for force field parameterization face significant challenges with the rapid expansion of synthetically accessible chemical space. Recent efforts have leveraged machine learning techniques to address these limitations:

Data-Driven Force Fields: Modern approaches like ByteFF utilize large-scale, high-diversity quantum mechanics datasets with sophisticated machine learning techniques. ByteFF employs an edge-augmented, symmetry-preserving molecular graph neural network trained on 2.4 million optimized molecular fragment geometries with analytical Hessian matrices and 3.2 million torsion profiles [8].

Hybrid Approaches: Methods like Espaloma introduce end-to-end workflows where MM force field parameters are predicted by graph neural networks, showing promise for improving transferability and accuracy across diverse chemical spaces [8].

Systematic Validation: Recent benchmarks of twelve popular and emerging fixed-charge force fields across curated peptide sets reveal that while some force fields exhibit strong structural bias and others allow reversible fluctuations, no single model performs optimally across all systems. This highlights limitations in current force fields' ability to balance disorder and secondary structure, particularly when modeling conformational selection [19].

Figure 2: Modern Data-Driven Force Field Development Workflow. Contemporary force field development involves generating diverse molecular datasets, performing quantum mechanical calculations, training machine learning models for parameter prediction, and rigorous validation through iterative refinement cycles.

Integrated Protocols for Molecular Dynamics Simulations

This section provides detailed methodologies for setting up and running molecular dynamics simulations using different software platforms, with a focus on reproducibility and performance optimization.

GROMACS Simulation Protocol

GROMACS is renowned for its exceptional performance and comprehensive toolset for biomolecular simulations [13] [14]. The following protocol outlines a standard production MD workflow:

System Preparation:

• Obtain protein structure from PDB database and process with pdb2gmx to generate topology: gmx pdb2gmx -f protein.pdb -o processed.gro -p topol.top
• Solvate the system in a water box using solvate: gmx solvate -cp protein.gro -cs spc216.gro -o solvated.gro -p topol.top
• Add ions to neutralize charge using genion: gmx genion -s em.tpr -o neutralized.gro -p topol.top -pname NA -nname CL -neutral

Energy Minimization:

• Run steepest descent energy minimization: gmx mdrun -deffnm em -ntomp ${SLURM_CPUS_PER_TASK:-1} -nb gpu -pme gpu

Equilibration:

• NVT equilibration for 100ps with position restraints on protein: gmx mdrun -deffnm nvt -ntomp ${SLURM_CPUS_PER_TASK:-1} -nb gpu -pme gpu
• NPT equilibration for 100ps with position restraints: gmx mdrun -deffnm npt -ntomp ${SLURM_CPUS_PER_TASK:-1} -nb gpu -pme gpu

Production MD: Execute production run with appropriate hardware resources:

Table 3: GROMACS Hardware Configuration Examples

Resource Level	CPU Cores	GPU Configuration	Memory	Use Case
Standard CPU	8 (2 tasks × 4 cpus-per-task)	None	4 GB per core	Medium-sized systems [20]
Single GPU	12 CPU cores	1 GPU (e.g., RTX 4090)	2 GB per core	Typical biomolecular systems [20]
Multi-GPU	24 (2 tasks × 12 cpus-per-task)	2 GPUs (e.g., A100)	2 GB per core	Large complexes, membrane systems [20]

Example submission script for single GPU simulation on HPC cluster:

AMBER Simulation Protocol

AMBER provides specialized tools for biomolecular simulations, with excellent performance on NVIDIA GPUs [18] [20]:

System Preparation:

• Use tleap to prepare topology and coordinate files: tleap -f system.in
• Solvate system with explicit water model: solvateOct system TIP3PBOX 10.0
• Add ions to neutralize system charge: addIons system Na+ 0 or addIons system Cl- 0

Energy Minimization:

• Run minimization in two stages: first with restraints on solute, then without restraints

Equilibration:

• Heat system gradually from 0K to target temperature over 50-100ps with weak restraints
• Density equilibration at constant pressure for 100-500ps

Production MD: Execute production run with PMEMD CUDA implementation:

Performance Optimization Strategies

Enhanced Sampling: Implement hydrogen mass repartitioning to enable 4fs time steps:

Multi-GPU Scaling: For appropriate workloads, multi-GPU configurations can significantly accelerate simulations. GROMACS shows good strong scaling across multiple GPUs for sufficiently large systems [18] [20].

CPU-GPU Workload Balance: Optimize distribution of different force calculation components between CPU and GPU. In GROMACS, using -nb gpu -pme gpu -update gpu -bonded cpu typically provides optimal performance [20].

Successful molecular dynamics simulations require both software tools and appropriate hardware resources. The following table details key components of the MD research toolkit:

Table 4: Essential Research Reagent Solutions for Molecular Dynamics

Resource Category	Specific Tools/Components	Function/Purpose	Application Context
MD Software	GROMACS, AMBER, NAMD, AMS	Core simulation engines	All-atom MD simulations [13] [15] [17]
Visualization & Analysis	VMD, PyMol, Chimera	Trajectory analysis, visualization	Result interpretation, publication figures [15]
Force Fields	AMBER, CHARMM, GAFF, OpenFF	Molecular mechanics potential functions	Defining interatomic interactions [15] [8]
Quantum Chemistry	Gaussian, ORCA, Quantum ESPRESSO	Reference calculations, parameterization	Force field development [17] [8]
System Preparation	PDB2GMX, tleap, packmol	Initial structure setup	Simulation initialization [13] [20]
HPC Resources	CPU clusters, GPU accelerators	Computational infrastructure	Production simulations [18] [20]
Specialized Hardware	NVIDIA RTX 6000 Ada, A100	GPU acceleration	Large-scale biomolecular simulations [18]
Workflow Tools	PLAMS, Jupyter notebooks	Automation, reproducibility	Protocol standardization, analysis [17]

The selection of appropriate molecular dynamics software and force fields represents a critical decision point in establishing reliable simulation protocols for scientific research and drug development. GROMACS stands out for its exceptional performance and active development cycle, while AMBER provides specialized tools for biomolecular systems. AMS offers comprehensive multi-scale modeling capabilities with strong graphical interfaces. For force fields, traditional options like AMBER and CHARMM remain well-validated for biomolecular applications, while data-driven approaches like ByteFF show promise for expansive chemical space coverage. As the field evolves, the integration of machine learning methods into both simulation algorithms and force field development is likely to further enhance the accuracy and scope of molecular dynamics investigations, particularly for drug discovery applications where understanding molecular interactions at atomic resolution provides critical insights. Researchers should select tools based on their specific system characteristics, accuracy requirements, and available computational resources, while remaining attentive to emerging methodologies that may offer advantages for particular applications.

In molecular dynamics (MD) simulations, creating a realistic simulation environment is paramount for obtaining biologically relevant results. The core of this environment is defined by three interconnected components: the application of periodic boundary conditions (PBC) to eliminate edge artifacts, the solvation of the molecular system to mimic its physiological context, and ion neutralization to achieve charge neutrality and physiological ionic strength. Together, these components form a periodic unit cell that serves as a minimal representation of a much larger, potentially infinite, system. This protocol details the theoretical underpinnings and practical procedures for establishing this environment, framed within the context of a broader thesis on MD simulation protocol research. It is tailored for researchers, scientists, and drug development professionals who require robust and reproducible simulation methodologies.

Theoretical Background

Periodic Boundary Conditions (PBC)

The classical method to minimize edge effects in a finite system is to apply periodic boundary conditions [21]. In this approach, the atoms of the system are placed in a primary simulation box, which is surrounded in all directions by translated copies of itself. These copies are termed periodic images. This construction effectively removes physical boundaries, meaning an atom leaving the box on one side simultaneously re-enters from the opposite side [21] [22].

Simulations operate under the minimum image convention, which stipulates that each atom interacts only with the closest image of any other atom in the system [21]. This convention is crucial for the correct calculation of short-range non-bonded interactions. For long-range electrostatic interactions, more sophisticated methods like the Particle Mesh Ewald (PME) algorithm are required [21] [23].

A critical consideration when using PBC is the cut-off radius ((R_c)) for short-range interactions. To satisfy the minimum image convention, the cut-off must not exceed half the length of the shortest box vector:

Furthermore, for efficiency in grid-based searching algorithms, an even stricter limitation may apply, such as (Rc < \min(ax, by, cz)) [21]. Violating these conditions can lead to unphysical interactions where an atom interacts with multiple images of the same atom.

Box Shapes

While a cubic box is the most intuitive, other space-filling shapes can be more efficient for simulating approximately spherical molecules, as they require fewer solvent molecules to fill the volume [21]. The most general space-filling shape is the triclinic box, which encompasses all other shapes. Table 1 compares common box types used in MD simulations.

Table 1: Characteristics of Common Periodic Box Types

Box Type	Image Distance	Box Volume (relative to cube)	Description
Cubic	(d)	(d^3) (100%)	A rectangular box with all sides equal and angles of 90°. Simple but least efficient for spherical solutes.
Rhombic Dodecahedron	(d)	(0.707d^3) (~71%)	The smallest and most regular space-filling unit cell. Saves ~29% solvent compared to a cube with the same image distance [21].
Truncated Octahedron	(d)	(0.770d^3) (~77%)	Closer to a sphere than a cube, offering savings in the number of required solvent molecules [21].

Solvation and Ion Neutralization

To mimic a physiological environment, the solvated system must be placed in an aqueous solution. This is achieved by explicitly filling the periodic box with water molecules. The choice of water model (e.g., TIP3P, TIP4P) is force-field dependent [23] [24].

Most biomolecules carry a net charge in solution. Simulating a charged periodic system is problematic because the PBC would sum the net charge of the unit cell with its images to infinity, leading to unrealistic electrostatic energies. Therefore, ion neutralization is essential. This involves adding sufficient counter-ions (e.g., Na⁺ for a negatively charged solute, Cl⁻ for a positively charged one) to bring the total net charge of the system to zero [24]. Beyond neutralization, additional salt ions can be added to mimic a specific physiological ionic strength (e.g., 150 mM NaCl) [23].

Protocol: Setting Up the Simulation Environment with GROMACS

This protocol provides a detailed workflow for setting up a simulation environment for a protein using the GROMACS MD suite [24]. The process is broadly applicable to other biomolecules like nucleic acids.

Preparation and System Setup

Step 1: Obtain and Prepare Protein Coordinates

• Download the protein structure of interest from the RCSB Protein Data Bank (http://www.rcsb.org).
• Visually inspect the structure using a molecular viewer (e.g., RasMol, VMD).
• Pre-process the structure: remove crystallographic water molecules and any non-standard ligands. If ligands are required, their topology must be generated separately.
• Use the pdb2gmx command to generate the molecule topology and coordinate file in GROMACS format. This step adds missing hydrogen atoms and allows you to select an appropriate force field (e.g., ffG53A7 for proteins with explicit solvent).

Step 2: Define the Periodic Box

• Use the editconf command to place the protein in the center of a periodic box. A cubic box with a minimum distance of 1.0 nm (10 Ã…) between the protein and the box edge is a common starting point. For a more spherical solute, a rhombic dodecahedron is more efficient [21] [24].

Solvation and Ion Neutralization

Step 3: Solvate the System

• Use the solvate command (also called gmx solvate in newer versions) to fill the box with water molecules. The topology file is automatically updated to include the water molecules.

Step 4: Add Ions

• First, generate a pre-processed input file (.tpr) using a parameter file (em.mdp) containing energy minimization settings.

• Use the genion command to replace water molecules with ions. The system is neutralized first, then additional ions are added to achieve the desired ionic concentration.

Table 2: Essential Research Reagent Solutions for MD Setup

Reagent / Material	Function / Description
Protein Structure File (.pdb)	The initial atomic coordinates of the biomolecule, obtained from the PDB or homology modeling.
Force Field (e.g., ffG53A7, AMBER-OL3)	A set of mathematical functions and parameters describing the potential energy of the system. Dictates the physical behavior of atoms [25] [24].
Water Model (e.g., TIP3P, TIP4P)	Explicit water molecules used to solvate the system, mimicking an aqueous biological environment [23] [24].
Ions (e.g., Na⁺, Cl⁻, K⁺)	Counter-ions for system neutralization and salt ions to mimic physiological ionic strength.

The following workflow diagram summarizes the key steps in setting up a simulation environment.

Application Example: RNA Stem-Loop in Explicit Solvent

A study on RNA stem-loop folding employed a protocol mirroring the one described above [23]. The initial A-form RNA structures were built for various sequences. Each system was first neutralized with a single Na⁺ ion, then solvated with 2000 TIP3P water molecules in a truncated octahedral box under PBC. This box shape was chosen for its computational efficiency relative to a cube. Finally, the system was brought to physiological conditions by adding five Na⁺ and Cl⁻ ions, resulting in a final Na⁺ concentration of 0.162 M. The structures were subsequently minimized and equilibrated before production MD runs, which used an 8.0 Å cut-off for non-bonded interactions and the Particle Mesh Ewald (PME) method for long-range electrostatics [23].

Analysis and Visualization

Understanding "Wrapping"

During an MD simulation, molecules can diffuse freely across the boundaries of the primary simulation box. Consequently, in the raw trajectory, a molecule of interest may appear to have left the box. This is normal and does not mean it is no longer interacting with the system; it has simply moved into a neighboring periodic image [22].

For visual clarity, it is common practice to "wrap" the trajectory, meaning all atoms are translated back into the primary box. This requires defining a center for the box, which is typically the center of mass of the solute (e.g., the protein). Wrapping around an arbitrary solvent molecule instead would cause the solute to be split across the box boundaries, creating a visually fragmented structure [22]. Tools like trjconv in GROMACS or the moleculekit Python library can perform this operation.

Advanced Protocols and Cutting-Edge Applications in Biomedicine

Molecular dynamics (MD) simulations serve as a crucial computational tool for studying the physical movements of atoms and molecules over time, providing invaluable insights into biomolecular structure, dynamics, and function at an atomic level. For researchers investigating proteins, peptides, and protein-ligand complexes, MD simulations bridge the gap between static structural data from X-ray crystallography or NMR and dynamic biological mechanisms [26] [27]. The efficacy of these simulations depends critically on appropriate protocol selection, careful system setup, and proper analysis techniques. Within the broader context of molecular dynamics simulation protocol research, this application note provides detailed methodologies for simulating biomolecular systems, focusing on practical implementation, hardware considerations, and emerging trends that enhance simulation accuracy and efficiency. The protocols outlined here emphasize reproducibility and statistical rigor, acknowledging that uncertainty in derived parameters depends not only on simulation data but also on analysis protocols and data processing decisions [28].

Essential Hardware and Software Infrastructure

Hardware Selection for Biomolecular Simulations

Selecting appropriate hardware is fundamental for efficient MD simulations. The computational intensity of these simulations requires careful balancing of CPU, GPU, and memory resources to achieve optimal performance without unnecessary expenditure.

Table 1: Recommended Hardware Configurations for Biomolecular MD Simulations

Component	Recommendation	Key Considerations	Example Models
CPU	Workstation-grade with high clock speeds	Prioritize clock speed over extreme core counts; sufficient PCIe lanes for multi-GPU setups	AMD Threadripper PRO 5995WX; Intel Xeon Scalable [29]
GPU	High-performance with substantial VRAM	CUDA core count; memory bandwidth; mixed-precision performance	NVIDIA RTX 6000 Ada (48 GB VRAM); NVIDIA RTX 4090 (24 GB GDDR6X) [29]
RAM	Capacity-matched to system size	Minimum 16 GB for setup; 128+ GB for production runs on large systems	DDR4/DDR5 with high bandwidth [26]
Storage	High-speed NVMe SSDs	Fast read/write for trajectory files (often terabytes)	PCIe 4.0/5.0 NVMe drives [30]

For molecular dynamics workloads, processors with higher base and boost clock speeds often outperform those with exceptionally high core counts, as many simulation codes rely on the speed at which a CPU can deliver instructions to other components [29]. Graphics Processing Units (GPUs) are particularly valuable for accelerating computationally intensive tasks in MD simulations. NVIDIA's Ada Lovelace architecture GPUs, such as the RTX 6000 Ada and RTX 4090, provide massive parallel processing power through thousands of CUDA cores, significantly reducing simulation time for popular MD software including AMBER, GROMACS, and NAMD [29]. The choice between these GPUs often depends on simulation size, with the RTX 6000 Ada's 48 GB of VRAM being particularly advantageous for large, complex biomolecular systems that require extensive memory resources [29].

Multi-GPU setups can dramatically enhance computational efficiency for appropriate workloads, allowing researchers to simulate larger systems or achieve faster turnaround times [29]. Additionally, cloud-based GPU solutions offer a flexible alternative to local hardware investments, particularly for projects with variable computational needs or limited infrastructure budgets [30].

Software Ecosystem

The MD software landscape includes both open-source and commercial packages, each with particular strengths for biomolecular simulations:

• GROMACS: A free, high-performance MD software suite known for its excellent parallelization and efficiency on both CPUs and GPUs, particularly for biomolecular systems [31].
• AMBER: A leading MD package specifically optimized for biomolecular simulations, with excellent NVIDIA GPU integration and specialized tools for MM-PBSA/GBSA calculations [27].
• NAMD: Recognized for its parallel scaling capabilities on large systems and efficient utilization of NVIDIA GPUs [29].
• LAMMPS: A versatile MD code with capabilities extending beyond biomolecules to materials modeling, with recent extensions for AI-driven simulations through interfaces like ML-IAP-Kokkos [32] [33].

Detailed Simulation Protocols

System Setup and Equilibration

Proper system setup is crucial for generating physically meaningful simulation results. The following protocol outlines key steps for preparing biomolecular systems, with specific examples for protein simulations using GROMACS.

Initial Structure Preparation

The simulation process begins with obtaining high-quality structural data. Protein structures can be sourced from the Protein Data Bank (PDB) or generated through homology modeling when experimental structures are unavailable [26]. The initial structure must be carefully prepared by:

• Removing extraneous molecules: Eliminate crystallographic water molecules and non-essential ligands that might interfere with the simulation setup [26].
• Adding hydrogen atoms: Most MD packages automatically add hydrogens, which are often missing from PDB structures [26].
• Handling specialized residues: For non-standard residues or ligands, separate topology files must be created and integrated into the main molecular description [26].

The following GROMACS command converts a PDB file to GROMACS format while generating topology and adding hydrogens:

This command prompts users to select an appropriate force field, with "ffG53A7" being recommended for protein simulations with explicit solvent in GROMACS v5.1 [26].

Solvation and Ion Placement

Biomolecular simulations require solvation to mimic physiological conditions. After defining the simulation box with periodic boundary conditions to minimize edge effects, the system is solvated with water molecules [26]. The following command adds water molecules to the simulation box:

The topology file is automatically updated to include water molecules [26]. After solvation, the system must be neutralized by adding counterions based on the total charge calculation:

This command adds ions to neutralize the system—in this example, three anions to counter a +3.00 net charge [26].

Energy Minimization and Equilibration

Before production simulations, the system must undergo energy minimization to remove steric clashes and unfavorable interactions, followed by careful equilibration to stabilize temperature and pressure. The GROMACS grompp command collects parameters, topology, and coordinates into a single input file:

The resulting file (.tpr) contains the complete molecular description for simulation steps [26]. After minimization, systems typically undergo equilibration in stages—first with position restraints on the biomolecule while solvent relaxes (NVT ensemble for temperature stabilization), followed by full system equilibration without restraints (NPT ensemble for pressure stabilization).

Production Simulation and Analysis

Production simulations generate the trajectory data used for analysis, often running for nanoseconds to microseconds depending on the biological process being studied. For most biomolecular systems, the NPT ensemble (constant Number of particles, Pressure, and Temperature) is used to mimic physiological conditions.

Analysis Methods

After production simulations, various analysis techniques extract biologically relevant information:

• Root Mean Square Deviation (RMSD): Measures structural stability by calculating the average distance between atoms of superimposed structures.
• Root Mean Square Fluctuation (RMSF): Quantifies flexibility of specific residues or regions over the simulation trajectory.
• Principal Component Analysis (PCA): Identifies collective motions and essential dynamics by reducing trajectory dimensionality [27].
• MM-PBSA/GBSA: Calculates binding free energies for protein-ligand complexes using Molecular Mechanics/Poisson-Boltzmann (Generalized Born) Surface Area approaches [27].

Table 2: Key Analysis Methods for Biomolecular Trajectories

Analysis Method	Application	Software Tools	Key Outputs
RMSD	Structural stability	GROMACS, AMBER, VMD	Convergence; structural drift
RMSF	Residual flexibility	GROMACS, CPPTRAJ	Flexible regions; binding sites
H-bond analysis	Interaction networks	GROMACS, VMD	Persistent interactions
PCA	Collective motions	GROMACS, Bio3D	Essential dynamics; conformational sampling
MM-PBSA/GBSA	Binding affinities	AMBER, GROMACS	Estimated binding free energies [27]

Uncertainty Quantification

When deriving quantitative parameters such as diffusion coefficients from mean-squared displacement (MSD) data, researchers must recognize that uncertainty depends not only on simulation data but also on the choice of statistical estimator (OLS, WLS, GLS) and data processing decisions including fitting window selection and time-averaging approaches [28]. Proper uncertainty estimation requires careful attention to these analysis protocol details rather than treating uncertainty as inherent solely to the simulation data.

Advanced Applications and Emerging Methodologies

Multiscale Simulation Approaches

Advanced simulation strategies combine multiple computational techniques to address complex biological questions while managing computational costs. Recent methodologies integrate Brownian dynamics (BD) with all-atom MD simulations to compute protein-ligand association rates, leveraging the strengths of each approach [34]. BD efficiently simulates long-range diffusion and encounter complex formation, while MD captures short-range interactions and molecular flexibility with atomic detail [34]. This multiscale approach generates accurate association rate constants (k_on) that align well with experimental data while remaining computationally feasible compared to pure MD approaches [34].

Multiscale simulation workflow combining Brownian dynamics and molecular dynamics.

AI-Enhanced Molecular Dynamics

Machine learning approaches are revolutionizing biomolecular simulations by dramatically increasing speed while maintaining accuracy. Neural network potentials like Egret-1 and AIMNet2 match or exceed quantum-mechanics-based simulation accuracy while running orders-of-magnitude faster [35]. These AI-driven approaches enable simulations that were previously computationally prohibitive, allowing researchers to explore longer timescales and larger systems.

The integration of PyTorch-based machine learning interatomic potentials (MLIPs) with traditional MD packages like LAMMPS through interfaces such as ML-IAP-Kokkos represents a significant advancement [33]. This interface uses Cython to bridge Python and C++/Kokkos LAMMPS, ensuring end-to-end GPU acceleration while maintaining the flexibility of Python-based model development [33]. For researchers, this means the ability to incorporate sophisticated machine learning potentials into production simulations without sacrificing performance.

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 3: Essential Research Reagents and Computational Tools for Biomolecular MD Simulations

Item	Function/Application	Examples/Sources
Protein Structure Coordinates	Starting structures for simulations	RCSB Protein Data Bank (http://www.rcsb.org/) [26]
Force Fields	Molecular mechanics parameters for energy calculations	ffG53A7 (GROMACS); AMBER force fields; CHARMM [26] [27]
Molecular Topology Files	Molecular description including bonding, angles, charges	Generated by pdb2gmx; manually edited for ligands [26]
Parameter Files (.mdp)	Simulation parameters including integrator, temperature, pressure	GROMACS website; customized for specific protocols [26]
Visualization Software	Trajectory analysis and rendering	Rasmol; VMD; PyMOL [26]
Quantum Chemistry Data	Parameterization of novel molecules or validation	DFT calculations; reference quantum chemical calculations [27]
(E)-isopentadec-2-enoyl-CoA	(E)-isopentadec-2-enoyl-CoA, MF:C36H62N7O17P3S, MW:989.9 g/mol	Chemical Reagent
M-Peg9-4-nitrophenyl carbonate	M-Peg9-4-nitrophenyl carbonate, MF:C24H39NO13, MW:549.6 g/mol	Chemical Reagent

This application note has detailed comprehensive protocols for simulating biomolecular systems, emphasizing the integrated nature of hardware selection, system setup, production simulation, and analysis. The field of molecular dynamics continues to evolve rapidly, with emerging trends including AI-enhanced simulations, multiscale approaches, and improved uncertainty quantification shaping future methodologies. By adhering to rigorous protocols and maintaining thorough documentation of each simulation step—including software versions, parameters, and analysis methods—researchers can ensure reproducible, scientifically valid results that advance our understanding of biomolecular systems and facilitate drug development efforts.

Molecular dynamics (MD) simulations have emerged as indispensable tools in the rational design of complex drug delivery systems, particularly lipid nanoparticles (LNPs) and polymeric nanoparticles. The multi-scale and multi-parameter complexity of these nanocarriers makes computational approaches essential for bridging the gap between fundamental molecular properties and therapeutic efficacy [36]. LNPs represent extremely complex systems with nearly infinite design variables, making traditional experimental approaches alone insufficient for fully understanding and optimizing their performance [36]. MD simulations provide a powerful complementary tool that allows researchers to explore vast chemical and physical spaces efficiently, systematically modeling key interactions and predicting functional outcomes that would be impractical or impossible to achieve solely through experiments [36].

The hierarchical nature of LNP performance spans multiple scales—from molecular lipid chemistry and self-assembly mechanisms to particle morphology and in vivo pharmacokinetics—each requiring different computational approaches to extract meaningful insights [36]. Physics-based modeling, including computational quantum chemistry, all-atom and coarse-grained MD simulations, and computational fluid dynamics, offers unparalleled molecular and submolecular insights into LNP behavior, enabling investigators to study structural dynamics, lipid-RNA interactions, and endosomal escape mechanisms at a level of detail inaccessible to experimental methods [36]. This application note details specific MD methodologies, protocols, and applications for advancing LNP and polymer-based drug delivery system design within the broader context of molecular dynamics simulation protocol research.

MD Methodologies for Nanoparticle Characterization

All-Atom Molecular Dynamics (AA-MD)

All-atom MD simulations provide the highest resolution approach for investigating LNP structure and dynamics by explicitly modeling every atom in the system. AA-MD is particularly valuable for studying lipid membranes and membrane-protein interactions, with numerous applications aimed at enhancing understanding of membrane dynamics, membrane remodeling processes, and membrane proteins [36]. Recent applications of AA-MD models to examine LNP structure and dynamics have revealed crucial insights, though accurately modeling the protonation states of ionizable lipids in various membrane environments remains challenging [36].

The protonation states of ionizable lipids in LNPs are environment-dependent when the pKa values of ionizable sites are near the solution pH, significantly influencing overall LNP charge and interactions with biological systems [36]. To address this challenge, constant pH molecular dynamics (CpHMD) models have been developed, with scalable CpHMD implementations now performing at speeds comparable to standard MD models [36]. These methods implement λ-dynamics based on the linear interpolation of partial charges between protonated and deprotonated states of appropriately parameterized ionizable sites, enabling hundreds of ionizable sites to be modeled simultaneously [36]. Recent applications have demonstrated that CpHMD models can accurately reproduce apparent pKa values for different LNP formulations with mean average errors of 0.5 pKa units [36].

A key strength of atomistic adaptive membrane models is their accuracy in capturing complex supramolecular interactions, such as the hydrophobic effect that dictates membrane self-assembly [36]. However, the explicit treatment of all atoms, particularly solvent molecules that often constitute more than 70% of total atoms, incurs high computational costs [36]. These challenges can be partially addressed by establishing reduced model systems, such as bilayer or multilamellar membrane models combined with periodic boundary conditions to approximate larger LNP structures [36]. Enhanced sampling techniques—including umbrella sampling, metadynamics, replica exchange MD, steered MD, and biased MD—can be employed to model events occurring on timescales exceeding current AA-MD capabilities, enabling simulation of rare events crucial for LNP function such as membrane reorganization during manufacturing or endosomal release of LNP-encapsulated RNA [36].

Coarse-Grained Molecular Dynamics (CG-MD)

Coarse-grained MD simulations represent groups of atoms by simplified interaction sites, enabling modeling of larger systems and longer timescales compared to AA-MD simulations [36]. CG-MD helps researchers understand detailed molecular structures and LNP mechanisms that are often difficult to characterize experimentally [36]. The level of coarse-graining varies significantly across models, ranging from highly simplified representations (1-3 CG sites per lipid) to relatively fine-grained approaches (over 6 sites per lipid) such as the popular Martini force field [36].

Table 1: Comparison of MD Simulation Approaches for LNP Research

Parameter	All-Atom MD	Coarse-Grained MD	Enhanced Sampling MD
Spatial Resolution	Atomic-level (0.1-1 nm)	Molecular group level (1-5 nm)	Varies (atomic to molecular)
Timescale Coverage	Nanoseconds to microseconds	Microseconds to milliseconds	Microseconds to seconds
System Size Limit	~100,000-1,000,000 atoms	~1,000,000-10,000,000 atoms	Similar to AA-MD or CG-MD
Key Applications	Lipid protonation states, atomic interactions	Self-assembly, large-scale morphology	Rare events, energy barriers
Computational Cost	High	Moderate	High (per simulation)
Enhanced Sampling	Limited without specialized methods	Limited without specialized methods	Specialized for rare events

Multiscale and Enhanced Sampling Approaches

Multiscale modeling frameworks represent the cutting edge of computational LNP research, hierarchically combining models at different resolutions to explore systems over larger time and spatial scales without sacrificing atomic-level accuracy [36]. Machine learning and artificial intelligence play increasingly crucial roles in these efforts, facilitating effective feature representation and linking various models for coarse-graining and back-mapping tasks [36].

Enhanced sampling techniques are specifically designed to improve sampling of rare events during MD simulations that would otherwise be extremely difficult to observe within limited classical MD timeframes [36]. However, each collective variable sampled using enhanced sampling methods incurs significant additional computational costs, restricting the number of CVs that can be efficiently sampled [36]. Furthermore, defining reasonable CVs for enhanced sampling often requires hypotheses about molecular mechanisms, making simulation outcomes dependent on initial assumptions and potentially hindering exploration of potential energy surfaces for CVs not well-represented in the selected set [36].

Quantitative MD Applications in LNP Optimization

LNP Self-Assembly and mRNA Encapsulation

MD simulations have provided crucial insights into LNP self-assembly mechanisms and mRNA encapsulation processes. Recent studies employing AA-MD simulations based on the lipid components and ratios of mRNA-1273 vaccines have demonstrated that lipid components self-assemble into nanoparticles under neutral conditions, with ionizable lipid SM-102 predominantly concentrating in the particle core [37]. Upon mixing with nucleic acids in acidic conditions, LNPs undergo disassembly, during which protonated SM-102 encapsulates mRNA through electrostatic interactions, forming stable hydrogen bonds [37].

Cluster structure analysis has revealed that the four lipid components in clinical LNPs distribute sequentially from outside to inside as DMG-PEG 2000, DSPC, cholesterol, and protonated SM-102 [37]. Furthermore, studies investigating different N/P ratios and acid types in nucleic acid solutions have demonstrated that LNPs constructed under low pH or low N/P ratios using citric acid exhibit larger volumes and more uniform distribution [37]. These findings provide scientific basis for optimizing LNP components to enhance mRNA vaccine encapsulation efficacy.

Table 2: Key Structural and Performance Parameters from LNP MD Simulations

Parameter	Simulation Findings	Experimental Correlation	Impact on LNP Performance
Ionizable Lipid Localization	SM-102 concentrates in particle core [37]	Enhanced encapsulation efficiency	Improves mRNA protection and endosomal escape
Component Distribution	Sequential distribution from outside: DMG-PEG 2000, DSPC, cholesterol, protonated SM-102 [37]	Affects LNP stability and cellular uptake	Optimizes structural integrity and drug release
Particle Size	100-190 nm diameter range [38]	Narrow size distribution (PdI <0.2)	Influences biodistribution and cellular targeting
Protonation State	Environment-dependent pKa values [36]	Affects LNP surface charge	Crucial for endosomal escape and mRNA release
mRNA Encapsulation	Electrostatic interactions with protonated lipids [37]	>85% encapsulation efficiency [38]	Determines therapeutic payload protection

Enhancing Endosomal Escape Mechanisms

Endosomal escape represents a critical bottleneck in LNP-mediated nucleic acid delivery, with only a small percentage of internalized nucleic acids successfully reaching the cytoplasm [38]. Recent MD investigations have explored innovative strategies to enhance this process, including the incorporation of cyclic disulfide-containing lipids (CDLs) into LNP formulations [38]. Studies demonstrate that CDL-incorporated LNPs achieve more than 2-fold higher transfection efficiency compared to LNPs with MC3 or SM102 alone, with intracellular analysis revealing that CDL additions significantly promote endosomal escape [38].

The mechanism behind enhanced endosomal escape involves cyclic disulfides with high ring tension (such as those derived from α-lipoic acid) that exhibit enhanced thiol-mediated membrane permeability compared to linear disulfides [38]. This approach differs fundamentally from conventional strategies that introduce disulfide bonds into fatty acid chains to facilitate intracellular degradation and payload release [38]. In vivo demonstrations have confirmed that CDL-incorporated LNPs administered subcutaneously in mice show significantly higher luciferase gene expression compared to LNPs without CDL, and LNPs encapsulating OVA antigen-encoding mRNA induce potent antitumor responses against lymphoma models [38].

Experimental Protocols

Protocol 1: AA-MD Simulation of LNP Self-Assembly

Objective: To simulate and analyze the self-assembly process of LNPs and their interaction with mRNA using all-atom molecular dynamics.

Materials and Software:

• Simulation Software: GROMACS, NAMD, or AMBER
• Force Field: CHARMM36, Lipid21, or GAFFlipid
• Visualization Tools: VMD, PyMOL
• Lipid Components: Ionizable lipids (SM-102, MC3), phospholipids (DSPC), cholesterol, PEG-lipids (DMG-PEG 2000)
• mRNA Sequence: Polyadenylated mRNA or specific antigen-encoding sequences

Methodology:

• System Construction:
  • Create initial coordinates for lipid molecules using molecular building tools (Packmol, CHARMM-GUI)
  • Set up simulation boxes with lipid:ethanol solution ratios reflecting experimental conditions (e.g., 30:50 ionizable lipid content) [37]
  • Implement periodic boundary conditions to approximate larger LNP structures [36]

• Parameterization:

  • Apply constant pH molecular dynamics (CpHMD) parameters for ionizable lipids to model environment-dependent protonation states [36]
  • Implement λ-dynamics for linear interpolation of partial charges between protonated and deprotonated states [36]
  • Set up electrostatic interactions using Particle Mesh Ewald method

• Simulation Protocol:

  • Energy minimization using steepest descent algorithm (5,000-10,000 steps)
  • Equilibration in NVT ensemble (100 ps, 300 K) with position restraints on lipid atoms
  • Equilibration in NPT ensemble (100 ps, 1 atm) with semi-isotropic pressure coupling
  • Production run (100 ns-1 μs) with 2 fs time step
  • Maintain temperature using Nosé-Hoover thermostat and pressure using Parrinello-Rahman barostat

• Analysis:

  • Calculate density distributions of lipid components relative to LNP center
  • Determine radial distribution functions between lipid headgroups and mRNA phosphate groups
  • Analyze solvent-accessible surface area (SASA) of mRNA throughout simulation
  • Perform cluster analysis to identify predominant structural arrangements

Protocol 2: CDL-LNP Formulation and Evaluation

Objective: To design, formulate, and evaluate cyclic disulfide-containing lipid nanoparticles for enhanced mRNA delivery and endosomal escape.

Materials:

• Lipid Components: CDL library with varying alkyl chain lengths (C16-C20), ionizable lipids (MC3, SM102), DOPE, cholesterol, DMG-PEG2k [38]
• mRNA: Luciferase-encoding mRNA or antigen-encoding mRNA (e.g., OVA)
• Formulation Equipment: Microfluidic mixer, dialysis membranes
• Analytical Instruments: DLS for size measurement, TEM for morphology, fluorescence spectroscopy for encapsulation efficiency

Methodology:

• CDL Synthesis:
  • Start with triethanolamine as base structure
  • Condense with fatty acids of varying chain lengths (C16, C18, C20), unsaturation (0, 1, or 2 bonds), and branching using DCC and DMAP
  • React intermediate with α-lipoic acid using DCC and DMAP to yield cyclic disulfide-containing lipids [38]

• LNP Formulation:

  • Prepare lipid mixtures with molar ratios: ionizable lipid (30 mol%), CDL (20 mol%), DOPE (10 mol%), cholesterol (38.5 mol%), DMG-PEG2k (1.5 mol%) [38]
  • Dissolve lipids in ethanol and mRNA in acidic buffer (pH 4.0)
  • Mix using microfluidic device with total flow rate 12 mL/min and flow rate ratio 3:1 (aqueous:organic)
  • Dialyze against PBS (pH 7.4) to remove ethanol and concentrate LNPs

• Characterization:

  • Measure particle size, polydispersity index, and zeta potential using dynamic light scattering
  • Determine mRNA encapsulation efficiency using Ribogreen assay
  • Evaluate in vitro transfection efficiency in relevant cell lines
  • Assess intracellular trafficking and endosomal escape using confocal microscopy

• In Vivo Evaluation:

  • Administer CDL-LNPs subcutaneously in mouse models
  • Measure luciferase expression using IVIS imaging
  • Evaluate antitumor efficacy in lymphoma models using OVA-encoding mRNA

Visualization of MD Workflows and LNP Mechanisms

Multiscale Modeling Framework for LNP Design

LNP Self-Assembly and mRNA Encapsulation Mechanism

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Research Reagents for LNP MD Simulations and Experimental Validation

Reagent Category	Specific Examples	Function and Application	Simulation Parameters
Ionizable Lipids	SM-102, MC3, DLin-MC3-DMA	Primary cationic component for mRNA complexation; enables endosomal escape through pH-dependent protonation [37] [38]	pKa 6.2-6.8; CpHMD parameters; λ-dynamics for protonation states [36]
Structural Lipids	DSPC, DOPE, Cholesterol	Enhance structural integrity, modify membrane fluidity, and improve stability [37] [39]	CHARMM36/Lipid21 parameters; bilayer formation properties; optimized mixing ratios [36]
PEGylated Lipids	DMG-PEG2000, DSG-PEG2000	Reduce immune recognition, prevent aggregation, control particle size [37] [38]	1.5-3.0 mol% in formulations; surface coverage parameters; steric stabilization models [36]
Specialty Lipids	Cyclic Disulfide Lipids (CDLs)	Enhance endosomal escape through thiol-mediated permeability; improve transfection efficiency [38]	Branching alkyl chains (C16-C20); cyclic disulfide moieties; 20 mol% incorporation [38]
Nucleic Acid Payloads	mRNA, siRNA, pDNA	Therapeutic cargo; chemical modifications enhance stability and reduce immunogenicity [40] [41]	Coarse-grained nucleotide models; electrostatic interaction parameters; encapsulation efficiency >85% [37]
Buffer Components	Citric Acid, Acetic Acid, Sucrose	Control pH during formulation; cryoprotection for lyophilization; affect LNP size and distribution [37]	pH 4.0 for encapsulation; ionic strength parameters; cryoprotectant interaction models [37]
3-Oxo-19-methyleicosanoyl-CoA	3-Oxo-19-methyleicosanoyl-CoA, MF:C42H74N7O18P3S, MW:1090.1 g/mol	Chemical Reagent	Bench Chemicals
Methyl threo-9,10-Dihydroxyoctadecanoate	Methyl threo-9,10-Dihydroxyoctadecanoate, MF:C19H38O4, MW:330.5 g/mol	Chemical Reagent	Bench Chemicals

Molecular dynamics (MD) simulations provide invaluable atomistic insights into chemical and biological processes but are fundamentally constrained by their accessible timescales. Many processes of biological and pharmaceutical interest, such as protein folding and conformational changes, occur on timescales much longer than what can be simulated with conventional MD. Enhanced sampling techniques have emerged as essential computational tools that overcome these limitations by accelerating the exploration of configuration space and facilitating the calculation of free energies. These methods can be broadly categorized into two families: collective variable (CV)-based methods such as metadynamics, which bias the simulation along preselected degrees of freedom, and generalized ensemble methods such as replica exchange, which expand the sampling space through non-physical pathways by modifying temperatures or Hamiltonians [42] [43]. The selection between these approaches represents a critical strategic decision in simulation protocol design, balancing the need for prior system knowledge against computational efficiency. This application note provides a comprehensive technical framework for implementing these powerful techniques, complete with structured quantitative comparisons and detailed experimental protocols tailored for research scientists and drug development professionals.

Theoretical Foundations

Replica Exchange Molecular Dynamics (REMD)

Replica exchange molecular dynamics (REMD) operates by simulating multiple non-interacting replicas of a system at different temperatures or with modified Hamiltonians [44]. At regular intervals, exchanges between neighboring replicas are attempted with an acceptance probability that preserves the correct Boltzmann distribution. For temperature REMD (T-REMD), this probability is calculated as:

[P(1 \leftrightarrow 2)=\min\left(1,\exp\left[ \left(\frac{1}{kB T1} - \frac{1}{kB T2}\right)(U1 - U2) \right] \right)]

where (T1) and (T2) are the reference temperatures and (U1) and (U2) are the instantaneous potential energies of replicas 1 and 2, respectively [44]. For simulations employing pressure coupling, an extension to the isobaric-isothermal ensemble incorporates volume changes:

[P(1 \leftrightarrow 2)=\min\left(1,\exp\left[ \left(\frac{1}{kB T1} - \frac{1}{kB T2}\right)(U1 - U2) + \left(\frac{P1}{kB T1} - \frac{P2}{kB T2}\right)\left(V1-V2\right) \right] \right)]

where (P1) and (P2) are reference pressures and (V1) and (V2) are instantaneous volumes [44].

Hamiltonian replica exchange (HREX) modifies the approach by creating replicas with different Hamiltonians, typically defined along an alchemical pathway. The exchange probability becomes:

[P(1 \leftrightarrow 2)=\min\left(1,\exp\left[ \frac{1}{kB T} (U1(x1) - U1(x2) + U2(x2) - U2(x_1)) \right]\right)]

where (U1) and (U2) represent different potential energy functions [44]. This approach is particularly valuable in free energy calculations and for systems where temperature changes would adversely affect the potential energy landscape.

Table 1: Replica Exchange Variants and Their Applications

Method Variant	Key Equation Parameters	Primary Applications	Computational Considerations
Temperature REMD	T₁, T₂, U₁, U₂	Protein folding, conformational transitions	Requires careful temperature spacing; number of replicas scales with system size
Hamiltonian REMD	U₁(x), U₂(x)	Alchemical free energy calculations, solvation free energies	Fewer replicas needed than T-REMD for large systems; requires λ-state definition
Gibbs Sampling REMD	All possible pairs exchange	Complex landscapes with multiple minima	No extra energy calculations; increased communication cost
Replica Exchange of Expanded Ensembles (REXEE)	Overlapping alchemical state sets	Multi-topology transformations, binding free energies	Decouples replica count from state count; enhanced parallelization

Metadynamics

Metadynamics accelerates sampling by adding a history-dependent bias potential to the system's Hamiltonian along selected collective variables (CVs). This bias, typically composed of Gaussian deposits, discourages the system from revisiting previously sampled configurations [45]. The free energy surface is recovered from the negative of the accumulated bias, providing crucial thermodynamic information. The efficiency of metadynamics hinges critically on the selection of appropriate CVs that capture the slow modes of the system. Suboptimal CV choice can lead to hysteresis and inaccurate free energy estimates [46].

The fundamental relationship between the probability distribution along a CV and the free energy is:

[A(\xi)=-{k}_{{{{\rm{B}}}}}T\ln(p(\xi))+C]

where (A(\xi)) is the free energy, (p(\xi)) is the probability distribution, and C is a constant [45]. Modern implementations like well-tempered metadynamics introduce a tempering factor that gradually reduces the height of added Gaussians, ensuring better convergence properties.

Integrated Methodological Approaches

Combining Metadynamics with Stochastic Resetting

Recent advances have demonstrated that metadynamics can be effectively combined with stochastic resetting (SR) to achieve significantly greater acceleration than either method alone [46]. In this hybrid approach, simulations are periodically stopped and restarted from independent and identically distributed initial conditions while resetting the metadynamics bias. This combination proves particularly valuable when working with suboptimal CVs, where resetting can achieve speedups comparable to those obtained with optimal CVs [46].

The effectiveness of SR depends on the distribution of transition times, with optimal acceleration occurring when the coefficient of variation (COV) – the ratio of the standard deviation to the mean first-passage time – is greater than one [46]. Metadynamics itself can alter the FPT distribution, increasing the COV and thereby creating conditions where SR provides additional acceleration. This hybrid approach demonstrates minimal sensitivity to initial conditions while reducing the risk of excessive bias deposition that can hamper convergence in aggressive metadynamics protocols [46].

Hamiltonian Replica Exchange with Generative Models

The integration of Hamiltonian replica exchange with diffusion-based generative models represents a cutting-edge approach to enhance sampling of biomolecular conformational landscapes. Recent work has adapted denoising diffusion probabilistic models (DDPMs) to the Hamiltonian replica exchange with solute tempering (REST2) framework [42]. This hybrid methodology treats potential energy as a fluctuating variable, allowing DDPMs to learn the joint probability distribution in configuration and rescaled potential energy space.

The diffusion process involves a forward noising step:

[q(\mathbf{xt}|\mathbf{x{t-1}}) = \mathcal{N}\left(\mathbf{xt};\sqrt{1-\betat}\mathbf{x{t-1}},\betat\mathbf{I}\right)]

and a learned reverse denoising process that generates configurations with accurate Boltzmann weights [42]. For systems where relevant reaction coordinates can be identified, an iterative scheme combining replica exchange, DDPM, and importance sampling progressively refines free-energy surfaces, particularly improving resolution in high-barrier regions [42]. This approach has demonstrated efficacy in mapping complex transition pathways, such as loop motions in enzymes, with significantly reduced computational overhead compared to conventional replica exchange.

Replica Exchange of Expanded Ensembles (REXEE)

The REXEE method represents a sophisticated integration of Hamiltonian replica exchange and expanded ensemble approaches [43]. In this framework, multiple replicas of expanded ensemble simulations run in parallel, each sampling different yet overlapping sets of alchemical states. Periodic coordinate exchanges between replicas enhance sampling while decoupling the number of replicas from the number of alchemical states.

This architecture addresses key limitations of both parent methods: it reduces the wall time compared to serial expanded ensemble simulations and provides greater flexibility in parameter specification compared to traditional HREX [43]. The method is particularly valuable for complex free energy calculations requiring numerous intermediate states, such as multi-topology transformations in relative free energy calculations, where it maintains sampling across all state ranges even when weights are poorly converged.

Experimental Protocols and Implementation

Replica Exchange Setup and Optimization

Temperature Selection Protocol: For temperature REMD, optimal temperature spacing ensures sufficient exchange probabilities. The energy difference between neighboring temperatures can be approximated as:

[U1 - U2 = N{df} \frac{c}{2} kB (T1 - T2)]

where (N{df}) is the total number of degrees of freedom and (c) is approximately 1 for harmonic potentials and around 2 for protein/water systems [44]. For a target exchange probability of (e^{-2}\approx 0.135), the relative temperature spacing should be (\epsilon \approx 2/\sqrt{c\,N{df}}). With constrained bonds, (N{df} \approx 2\, N{atoms}), yielding (\epsilon \approx 1/\sqrt{N_{atoms}}) for (c = 2) [44]. Modern implementations like the REMD calculator in GROMACS can automatically propose temperature sets based on the system size and desired temperature range.

Exchange Attempt Protocol: Exchanges are typically attempted between neighboring temperatures at regular intervals, with alternating odd and even pairs to maintain detailed balance. For instance, with four replicas (0-1-2-3), pairs 0-1 and 2-3 exchange on odd attempts, while pair 1-2 exchanges on even attempts [44]. Exchange frequencies should balance communication overhead with sampling efficiency, typically every 100-1000 steps.

MPI Parallelization Requirements: REMD simulations require MPI installation and typically run each replica on a separate rank [44]. The computational efficiency depends on load balancing across replicas, with similar computational cost per replica.

Metadynamics Implementation Protocol

Collective Variable Selection: Identify CVs that distinguish between metastable states and describe transition pathways. Common CVs include distances, angles, dihedrals, root-mean-square deviation (RMSD), or coordination numbers. For complex systems, dimensionality reduction techniques or deep learning approaches may be necessary to identify relevant CVs [45].

Bias Parameters:

• Gaussian height: Typically 0.1-5 kJ/mol
• Gaussian width: Determined by the fluctuation of the CV in an unbiased simulation
• Deposition rate: Every 100-1000 steps
• Well-tempered factor: If using well-tempered metadynamics, values of 10-100 for the bias factor are common

Simulation Protocol:

• Equilibrate the system with conventional MD
• Initialize metadynamics with zero bias
• Add Gaussian potentials at regular intervals along the current CV values
• For well-tempered metadynamics, reduce Gaussian height over time according to the tempering schedule
• Continue until the system transitions multiple times between states or the free energy profile converges

Convergence Assessment: Monitor the time evolution of the bias potential; convergence is indicated when the bias grows uniformly across the CV space. For well-tempered metadynamics, the bias deposition rate decreases over time as the simulation converges.

Hybrid Metadynamics-Stochastic Resetting Protocol

• Perform initial metadynamics simulations to estimate the coefficient of variation (COV) of transition times
• If COV > 1, stochastic resetting will likely provide additional acceleration [46]
• Determine the optimal resetting rate through preliminary tests or estimation from the FPT distribution
• Implement resetting by periodically stopping the simulation and restarting from randomized initial conditions
• Reset the metadynamics bias to zero at each resetting event
• For kinetics inference, apply correction methods to recover unbiased mean first-passage times [46]

Table 2: Enhanced Sampling Implementation Checklist

Step	Action Item	Key Parameters	Validation Metrics
Pre-simulation	System preparation	Solvation, ionization, minimization	Energy stability, reasonable density
CV Selection	Identify collective variables	CV type, number, parameters	Ability to distinguish states, physical relevance
Method Selection	Choose enhanced sampling method	Temperature range, replica count, bias parameters	Expected barrier heights, system size
Equilibration	Equilibrate system	Duration, stability checks	Energy drift, structural stability
Production Run	Execute enhanced sampling	Simulation length, exchange frequency, bias deposition	Transition events, convergence monitoring
Analysis	Process results	Free energy estimation, error analysis	Profile convergence, statistical uncertainty

Research Reagent Solutions

Table 3: Essential Software Tools for Enhanced Sampling

Software Tool	Primary Function	Key Features	Implementation Examples
GROMACS	Molecular dynamics engine	REMD, Hamiltonian exchange, metadynamics	Temperature ladder setup, λ-states for alchemical sampling [44]
PySAGES	Enhanced sampling library	GPU acceleration, multiple methods, ML integration	Custom CV definition, method combination [45]
PLUMED	Enhanced sampling plugin	Extensive CV library, metadynamics variants	Free energy calculation, path collective variables
ensemble_md	REXEE management	Expanded ensemble replica exchange	Alchemical sampling setup, asynchronous parallelization [43]

Enhanced sampling techniques represent indispensable tools in the molecular simulator's toolkit, effectively extending the accessible timescales for studying complex biological processes. Metadynamics provides powerful biased sampling along collective variables, while replica exchange methods offer generalized ensemble approaches that require less prior knowledge of reaction coordinates. The emerging trend of combining these methods with each other and with machine learning approaches – such as metadynamics with stochastic resetting or replica exchange with diffusion models – demonstrates the dynamic evolution of the field toward increasingly efficient and automated sampling solutions. As these methodologies continue to mature and integrate with high-performance computing infrastructures, they promise to unlock new frontiers in molecular simulation, enabling previously intractable studies of complex biomolecular processes with direct relevance to drug discovery and materials design. The protocols and implementation guidelines presented here provide researchers with practical pathways to leverage these powerful techniques in their investigative workflows.

Molecular dynamics (MD) simulations have become indispensable tools in modern computational biology and drug discovery, capable of providing unprecedented atomic-level insight into the behavior of biological systems [47]. However, a fundamental challenge persists: many critical biological processes occur across a wide spectrum of spatial and temporal scales that no single simulation method can comprehensively capture [48]. All-atom molecular dynamics (AAMD) simulations explicitly represent every atom in a system, providing high-resolution details of molecular interactions, but they are computationally expensive, typically limiting simulations to nanosecond-microsecond timescales for most biologically relevant systems [47] [48]. In contrast, coarse-grained molecular dynamics (CG-MD) simulations group multiple atoms into single interaction sites or "beads," significantly reducing computational cost and enabling the simulation of larger systems and longer timescales, albeit with reduced atomic detail [49] [50].

Multiscale modeling emerges as a powerful paradigm that bridges these scales, combining the accuracy of high-resolution methods with the sampling efficiency of simplified models [48]. By integrating different levels of resolution, either through sequential simulation pipelines or through hybrid methods where different system components are simulated at different resolutions simultaneously, researchers can tackle complex biological questions that span from atomic interactions to cellular phenomena [51] [48]. This approach is particularly valuable in pharmaceutical research, where understanding drug action requires connecting molecular-level binding events to their functional consequences at the cellular level [51] [48].

Theoretical Framework and Scale Comparison

The core principle of multiscale modeling lies in selecting the appropriate resolution for the specific biological question at hand. AAMD provides the highest resolution, with explicit representation of all atoms, making it ideal for studying detailed interaction mechanisms, binding energetics, and conformational changes at the atomic level [47]. CG-MD, by simplifying the representation of the system, allows access to longer timescales and larger systems, making it suitable for studying processes like protein folding, large-scale conformational changes, and protein-protein interactions [49] [50].

The choice between these approaches involves careful consideration of trade-offs. AAMD simulations utilize detailed force fields that include terms for bonds, angles, dihedrals, and non-bonded interactions, requiring small integration time steps (1-2 femtoseconds) and substantial computational resources [47]. CG-MD force fields use simplified potential functions with fewer interaction sites, allowing for longer time steps (typically 10-20 femtoseconds) and dramatically reduced computational cost [50]. This enables the simulation of microsecond to millisecond timescales and much larger systems, though at the cost of losing atomic-level details [50].

Table 1: Comparison of All-Atom and Coarse-Grained MD Simulation Approaches

Feature	All-Atom MD (AAMD)	Coarse-Grained MD (CG-MD)
Resolution	Explicit representation of all atoms	Groups of atoms represented as single "beads"
Time Scale	Nanoseconds to microseconds [47]	Microseconds to milliseconds [50]
Time Step	1-2 femtoseconds [47]	10-20 femtoseconds [50]
Computational Cost	High	Significantly lower
Atomic Detail	High	Limited
Common Force Fields	AMBER (ff19SB [50]), CHARMM [47], GROMOS [47]	Martini 3 [50], SIRAH [50], UNRES [50]
Ideal Applications	Ligand binding, enzyme mechanisms, ion channel permeation	Protein folding, large complexes, membrane remodeling

Table 2: Practical Considerations for Method Selection

Consideration	All-Atom MD (AAMD)	Coarse-Grained MD (CG-MD)
System Size	Suitable for single proteins to moderate complexes	Suitable for large complexes, membranes, cellular scale
Process Timescale	Fast processes (ns-µs)	Slower processes (µs-ms and beyond)
Required Detail	Atomic interactions, precise geometries	Global conformations, large-scale dynamics
Sampling Needs	Limited conformational sampling	Enhanced conformational sampling
Validation	Direct comparison to structural experiments	Comparison to low-resolution data (SAXS, FRET)

Multiscale approaches can be implemented in various ways. Sequential multiscale modeling involves using information from higher-resolution simulations to parameterize lower-resolution models [48]. For example, the potential of mean force calculated from AAMD simulations can inform effective interactions in CG-MD models. Concurrent multiscale modeling employs different resolutions simultaneously in the same simulation, such as in QM/MM methods where a small region of interest (e.g., an enzyme active site) is treated with quantum mechanics while the surroundings are modeled with molecular mechanics [48]. These integrated approaches enable researchers to connect phenomena across scales, providing a more comprehensive understanding of complex biological systems than would be possible with any single method alone [51].

Protocols for Multiscale Simulations

All-Atom MD Simulation Protocol

System Setup and Preparation: Begin with an experimental protein structure from the Protein Data Bank or a validated homology model [47]. For the AMBER package, use the tleap module to add missing hydrogen atoms, solvate the system in an explicit solvent box (OPC water model recommended for IDPs [50]), and add ions to achieve physiological concentration and neutrality. For the GROMACS package, use pdb2gmx for structure conversion and topology generation, followed by grompp for preprocessing [50]. Employ the ff19SB force field for proteins, which has demonstrated improved performance for both folded and disordered proteins compared to older parameter sets [50].

Energy Minimization and Equilibration: Perform energy minimization using steepest descent or conjugate gradient algorithms to remove steric clashes [50]. Subsequently, conduct a multi-step equilibration protocol: (1) gradually heat the system from 0 K to the target temperature (e.g., 310 K) over 100-500 ps using velocity rescaling or Langevin dynamics with harmonic positional restraints on protein heavy atoms (force constant of 5-10 kcal/mol/Ų), (2) maintain constant temperature and pressure (NPT ensemble) with reduced restraints for another 100-500 ps, and (3) run an additional 1-5 ns without restraints to ensure proper system equilibration [50].

Production Simulation and Analysis: Execute production simulations using a 2-fs time step with bonds involving hydrogen atoms constrained using LINCS (GROMACS) or SHAKE (AMBER) algorithms [47] [50]. Maintain constant temperature and pressure using appropriate thermostats (e.g., Nosé-Hoover) and barostats (e.g., Parrinello-Rahman). For enhanced sampling, consider running multiple independent trajectories or implementing replica exchange molecular dynamics (REMD) [50]. Analyze trajectories using tools integrated within simulation packages or specialized software to calculate properties such as root-mean-square deviation (RMSD), radius of gyration, secondary structure content, and interaction energies [50].

Coarse-Grained MD Simulation Protocol

System Conversion and Martini 3 Setup: For CG-MD simulations using the Martini 3 force field, convert all-atom structures to coarse-grained representation using the martinize.py script or similar tools [50]. For intrinsically disordered proteins (IDPs), apply protein-water interaction scaling (e.g., with a factor of 1.07-1.10) to prevent excessive compactness, a known issue with standard Martini parameters [50]. Solvate the system with standard Martini water beads and add ions as needed.

Equilibration and Production Run: Perform energy minimization followed by a two-step equilibration protocol: (1) run with position restraints on protein beads (force constant of 1000 kJ/mol/nm²) for 1-5 ns, and (2) run without restraints for an additional 5-10 ns [50]. Execute production simulations with a 10-20 fs time step [50]. For the SIRAH force field, follow similar protocols but using SIRAH-specific parameters and tools available through the AMBER or GROMACS packages [50].

Backmapping and Analysis: To recover atomistic details from CG trajectories, use backmapping tools such as backward.py for Martini or SIRAH-specific utilities [50]. Analyze CG trajectories using similar metrics as for AAMD, but adapted for coarse-grained representation, focusing on global properties such as large-scale conformational changes, protein-protein association, and membrane remodeling processes [49] [50].

Specialized Protocol: Dynamic Disulfide Bond Handling

For studies involving disulfide bonds, implement a dynamic approach using distance restraints rather than static bonds [50]. This allows for the simulation of disulfide bond formation and breakage under mechanical or environmental stress. Apply harmonic or flat-bottomed distance restraints between sulfur atoms of cysteine residues with equilibrium distances of 2.0-2.1 Å and appropriate force constants (e.g., 500-1000 kJ/mol/nm²) [50]. This method is particularly valuable for studying proteins under oxidative stress or mechanical force, and for understanding the role of disulfide bonds in protein stability and function [50].

Applications in Drug Discovery and Development

Multiscale MD simulations have made significant contributions to various stages of drug discovery and development, from target identification and validation to lead optimization and understanding drug resistance mechanisms [51] [47] [48].

Target Validation and Mechanism: In the early stages of drug discovery, MD simulations provide insights into the dynamics and function of potential drug targets [47]. For example, simulations of sirtuins, RAS proteins, and intrinsically disordered proteins have revealed conformational states and functional mechanisms that can be exploited for therapeutic intervention [47]. CG-MD simulations have been particularly valuable for studying large-scale conformational changes in these systems that occur on timescales inaccessible to AAMD [49] [47].

Binding Energetics and Kinetics: During lead discovery and optimization, MD simulations facilitate the evaluation of ligand-receptor interactions [47] [48]. Advanced sampling techniques such as metadynamics, Markov state models (MSMs), and milestoning enable the calculation of binding free energies and kinetics [48]. For instance, metadynamics simulations have been used to predict drug-target residence times, which increasingly are recognized as critical determinants of drug efficacy [48]. QM/MM approaches provide insights into electronic polarization effects during binding, which can significantly impact binding affinities and kinetics [48].

Membrane Protein Drug Targets: For membrane protein targets such as G-protein coupled receptors (GPCRs) and ion channels, multiscale approaches are particularly valuable [47] [48]. CG-MD simulations can model the association of drug molecules with membrane-bound targets, while AAMD simulations provide atomic-level details of drug binding modes and interactions [48]. These approaches have revealed the importance of membrane composition and dynamics for drug binding to membrane proteins [47].

Table 3: Multiscale Modeling Applications in Drug Discovery

Application Area	Methodology	Key Insights
Target Validation	CG-MD, AAMD	Revealed dynamics and conformational states of drug targets like sirtuins and RAS proteins [47]
Binding Kinetics	Metadynamics, MSM, Milestoning	Predicted drug-target residence times; revealed importance of kinetics over affinity for some drugs [48]
Membrane-Associated Drug Metabolism	Multiscale CG-AA-QM/MM	Showed membrane effects on channels and gating residues in cytochrome P450 enzymes [48]
Cardiac Drug Safety	Multiscale from atomic to tissue	Predicted emergent proarrhythmic drug effects not observable at single protein scale [51]
Antibody Design	AAMD, CG-MD	Provided insights into dynamics and interactions for engineering therapeutic antibodies [47]

The Scientist's Toolkit: Essential Research Reagents and Software

Table 4: Essential Software Tools for Multiscale Simulations

Tool/Software	Function	Application Context
GROMACS [47] [50]	High-performance MD simulation package	All-atom and coarse-grained simulations with excellent parallelization
AMBER [47] [50]	Suite of biomolecular simulation programs	All-atom simulations with extensive force fields and analysis tools
CHARMM [47]	Molecular simulation program	All-atom simulations with comprehensive force fields
NAMD [47]	Parallel MD simulation package	Large-scale all-atom and coarse-grained simulations
Martini 3 [50]	Coarse-grained force field	CG-MD simulations of proteins, lipids, carbohydrates
SIRAH [50]	Coarse-grained force field	CG-MD simulations compatible with AMBER and GROMACS
CP2K [50]	Quantum chemistry and solid-state physics software	Ab initio MD and QM/MM simulations
Ethyl 10(Z)-pentadecenoate	Ethyl 10(Z)-pentadecenoate, MF:C17H32O2, MW:268.4 g/mol	Chemical Reagent
9-hydroxyhexadecanoyl-CoA	9-hydroxyhexadecanoyl-CoA, MF:C37H66N7O18P3S, MW:1021.9 g/mol	Chemical Reagent

Table 5: Key Force Fields and Parameters

Force Field	Type	Recommended Use
ff19SB [50]	All-atom	State-of-the-art for proteins, including disordered regions
CHARMM36m [50]	All-atom	Optimized for membrane proteins and IDPs
OPC [50]	Water model	Recommended with ff19SB for IDPs
Martini 3 [50]	Coarse-grained	General-purpose CG-MD with protein-water scaling for IDPs
SIRAH [50]	Coarse-grained	CG-MD simulations with compatibility to AMBER/GROMACS

Multiscale modeling integrating coarse-grained and all-atom simulations represents a powerful framework for addressing complex biological questions in drug discovery and beyond. By strategically combining the sampling efficiency of CG-MD with the atomic precision of AAMD, researchers can bridge spatial and temporal scales to connect molecular-level events with their functional consequences. As force fields continue to improve, sampling algorithms become more efficient, and computational resources expand, the role of multiscale simulations in pharmaceutical research is poised to grow substantially. The protocols and applications outlined in this article provide a foundation for researchers to implement these powerful methods in their own investigations of biological systems and therapeutic interventions.

Solving Common MD Challenges: A Troubleshooting and Performance Optimization Guide

In molecular dynamics (MD) simulations, ensuring system stability through rigorous energy minimization, thermal equilibration, and precise control of temperature and pressure is a critical prerequisite for obtaining physically meaningful results. These foundational steps remove unrealistic atomic clashes, bring the system to target thermodynamic conditions, and maintain stability throughout production simulations. For researchers in computational chemistry and drug development, particularly those applying Model-Informed Drug Development (MIDD) approaches, robust simulation protocols provide essential quantitative insights into drug-target interactions and molecular behavior [52]. The stability of the simulation system directly impacts the reliability of predictions for critical development questions involving dose selection, clinical trial simulation, and safety evaluation [52].

This application note provides detailed protocols for achieving system stability, with structured tables comparing key parameters and visualization of complex workflows to guide researchers in implementing these critical procedures effectively.

Energy Minimization Methods and Parameters

Energy minimization resolves steric clashes and inappropriate geometry introduced during system construction by finding the nearest local energy minimum. This process relieves internal stresses and prepares the system for stable dynamics integration.

Comparative Analysis of Minimization Algorithms

Table 1: Energy Minimization Algorithms in Molecular Dynamics

Algorithm	Mathematical Basis	Convergence Tolerance (emtol)	Performance Characteristics	Optimal Use Cases
Steepest Descent	Follows negative energy gradient	Typically 10-1000 kJ·mol⁻¹·nm⁻¹	Robust for initial steps; slow near minimum [53]	Initial minimization of poorly structured systems
Conjugate Gradient	Sequential conjugate directions	Typically 10-1000 kJ·mol⁻¹·nm⁻¹	Faster convergence than steepest descent [53]	Intermediate minimization after steepest descent
L-BFGS	Low-memory Broyden–Fletcher–Goldfarb–Shanno	Typically 10-1000 kJ·mol⁻¹·nm⁻¹	Fastest convergence; limited parallelization [53]	Final minimization stages where high precision is required

Practical Implementation Protocol

Protocol 1: System Energy Minimization

• System Preparation: Construct simulation box with solvent and ions. Ensure periodic boundary conditions are properly defined.

• Algorithm Selection:

  • For initially distorted systems: Begin with integrator = steep for 50-100 steps [53]
  • Follow with integrator = cg for refined minimization [53]
  • For well-structured systems: Use integrator = l-bfgs for efficient convergence [53]

• Parameter Configuration:

  • Set emtol = 1000.0 for initial crude minimization
  • Set emtol = 10.0 for production-ready minimization
  • Define nsteps = -1 for tolerance-based convergence [53]

• Convergence Validation: Monitor potential energy and maximum force. The system is minimized when the maximum force is below emtol.

Figure 1: Sequential workflow for energy minimization employing multiple algorithms to achieve stable system configuration.

Thermal Equilibration Methodologies

Thermal equilibration brings the system to the target temperature while maintaining stability. The choice of thermostat and coupling strategy significantly impacts simulation quality and biological relevance.

Temperature Coupling Algorithms

Table 2: Temperature Control Parameters and Protocols

Thermostat	Algorithm Type	Integration Support	Time Constant (tau-t)	Application Context
Berendsen	Weak coupling	All integrators	0.1-1.0 ps	Initial heating; not for production [54]
Stochastic Dynamics	Leap-frog SD	integrator = sd	0.1-2.0 ps	Sampling canonical ensemble [53]
Langevin	Stochastic	All integrators	0.1-2.0 ps	Production runs; simplified systems [54]

Novel Solvent-Coupling Equilibration Protocol

Protocol 2: Solvent-First Thermal Equilibration

This protocol implements a physically motivated approach where only solvent atoms are coupled to the heat bath, allowing natural energy transfer to the solute [54].

• Initialization:

  • Set initial temperature to 0K
  • Apply position restraints to solute atoms
  • Couple only solvent atoms to heat bath [54]

• Gradual Heating:

  • Increase temperature from 0K to target (e.g., 300K) over 50-100ps
  • Maintain weak coupling to pressure bath (1 atm)

• Equilibration Monitoring:

  • Track temperature separately for solute and solvent
  • Continue until temperatures equalize (kinetic equilibrium) [54]
  • Remove position restraints after equilibrium is achieved

• Validation:

  • Verify equipartition of kinetic energy
  • Check root-mean-square deviation (RMSD) stability

Figure 2: Solvent-coupled thermal equilibration workflow where only solvent atoms contact the heat bath for natural energy transfer.

Pressure Control and Barostating

Pressure control maintains proper density and mimics experimental conditions. Barostat selection impacts ensemble correctness and simulation stability.

Pressure Coupling Schemes

Table 3: Pressure Control Parameters in MD Simulations

Barostat	Ensemble	Compressibility [bar⁻¹]	Time Constant (tau-p)	Algorithm Characteristics
Berendsen	NpT-like	4.5×10⁻⁵ (water)	0.5-2.0 ps	Efficient but incorrect fluctuations [54]
Parrinello-Rahman	NPT	4.5×10⁻⁵ (water)	1.0-5.0 ps	Correct fluctuations; sensitive to parameters [53]

Combined Thermostat-Barostat Implementation

Protocol 3: Coupled Temperature-Pressure Equilibration

• Initialization:

  • Start with thermally equilibrated system
  • Set target pressure (typically 1 bar)
  • Configure barostat with tau-p = 1.0-2.0

• Compressibility Setting:

  • For aqueous systems: compressibility = 4.5×10⁻⁵ bar⁻¹
  • For mixed systems: Adjust based on composition

• Anisotropic Control:

  • For membrane systems (e.g., PIM membranes for gas separation): Use semi-isotropic coupling [55]
  • For solution systems: Use isotropic coupling

• Stability Monitoring:

  • Track density fluctuations until stable
  • Verify box dimensions are not drifting systematically
  • Ensure potential energy remains stable

Integration Methods and Advanced Control

The choice of integration algorithm affects energy conservation, computational efficiency, and long-term stability.

Integrator Selection Guide

Table 4: Molecular Dynamics Integrators for Production Simulations

Integrator	Algorithm Basis	Time Step (fs)	Stability Characteristics	Recommended Applications
leap-frog (md)	Leap-frog Verlet	1-2 (2 with constraints)	Excellent for most systems [53]	Standard production simulations
velocity Verlet (md-vv)	Velocity Verlet	1-2 (2 with constraints)	Better energy conservation [53]	NVE simulations; advanced thermostats
stochastic (sd)	Stochastic Dynamics	1-2	Canonical sampling [53]	Explicit solvent canonical sampling

Mass Repartitioning for Enhanced Stability

Mass repartitioning enables longer time steps by scaling hydrogen masses and adjusting bonded heavy atoms:

• Set mass-repartition-factor = 3 for 3-fold hydrogen mass increase [53]
• With constraints = h-bonds, enables 4fs time steps [53]
• Maintains identical Hamiltonian while improving stability [53]

The Scientist's Toolkit: Essential Research Reagents

Table 5: Key Software Tools and Parameters for MD Simulations

Tool/Parameter	Function	Implementation Example
GROMACS	Molecular dynamics simulation package	gmx mdrun for simulation execution [53] [55]
mdp parameters	Simulation control parameters	integrator = md, dt = 0.002 [53]
Thermostat Algorithms	Temperature regulation	tcoupl = Berendsen, tau-t = 0.1 [53] [54]
Barostat Algorithms	Pressure regulation	pcoupl = Parrinello-Rahman, tau-p = 2.0 [53]
Langevin Dynamics	Stochastic temperature control	integrator = sd, ld-seed = -1 [53]
Constraint Algorithms	Bond length stabilization	constraints = h-bonds for 4fs time steps [53]

Application in Advanced Research Contexts

Stable MD protocols enable sophisticated applications in materials science and drug development. For example, in studying hydrocarbon ladder polymer membranes (Me2F and DHP) for COâ‚‚ separation, proper equilibration was essential for characterizing microporous structure and gas diffusion mechanisms [55]. The compression/relaxation strategy with 21-step gradual decompression at 600K maximum temperature and 50000 bar maximum pressure produced realistic polymer configurations for gas separation studies [55].

In drug development, the FDA's MIDD Paired Meeting Program highlights the regulatory importance of quantitative modeling and simulation approaches, which depend on reliable MD methodologies for assessing dose selection, clinical trial simulation, and safety evaluation [52]. These applications require exceptionally stable simulations to generate predictive results that inform regulatory decision-making.

Figure 3: Complete molecular dynamics stabilization protocol from initial structure to production simulation and analysis.

Molecular dynamics (MD) simulations have emerged as a powerful tool in biomedical research and materials science, enabling the study of physical movements of atoms and molecules over time [56]. The computational cost of these simulations is high, often requiring significant resources to model complex atomic interactions [57]. This application note provides a structured framework for optimizing MD performance through appropriate time step selection, hardware configuration, and parallelization strategies. The protocols outlined here are designed for researchers engaged in computational chemistry, biophysics, and drug development who need to maximize simulation efficiency and throughput while maintaining scientific accuracy [56] [58]. By implementing these guidelines, scientists can significantly accelerate their research workflows, from investigating protein-ligand interactions for drug discovery to designing advanced polymers for energy applications [56] [59].

Time Step Selection and Integration Algorithms

Fundamental Considerations for Time Step Selection

The time step (Δt) is a critical parameter in MD simulations that determines the interval between successive evaluations of the system's forces and positions. Selection of an appropriate time step must balance numerical stability with computational efficiency. Conventional MD simulations typically employ time steps of 1-2 femtoseconds (fs) when using velocity Verlet integration, which is sufficient to capture atomic vibrations and ensure energy conservation [60]. The maximum stable time step is primarily constrained by the highest frequency motions in the system, particularly bond vibrations involving hydrogen atoms. These fast motions require small time steps to accurately integrate, creating a bottleneck for simulating slow biological processes or materials behavior.

Advanced Integration Approaches

Constraint Algorithms and Multiple Time-Stepping: To enable longer time steps, constraint algorithms such as LINCS and P-LINCS are employed to freeze the fastest bond vibrations [61]. These algorithms allow time steps up to 2-4 fs while maintaining stability. The P-LINCS algorithm is particularly important for parallel simulations, as it efficiently handles constraints that cross domain boundaries in spatially decomposed systems [61]. Multiple time-stepping (MTS) schemes further enhance efficiency by evaluating computationally expensive non-bonded forces less frequently than fast bonded forces.

Machine Learning-Enhanced Integration: Recent advances propose using machine learning to create data-driven, structure-preserving maps that approximate long-time evolution of classical dynamical systems [62]. These ML integrators can potentially use time steps two orders of magnitude longer than conventional methods while maintaining symplectic properties and energy conservation. The approach involves learning the mechanical action of the system through generating functions, creating symplectic and time-reversible maps equivalent to the implicit midpoint rule [62]. This emerging methodology shows promise for dramatically accelerating simulations, though careful validation is required to ensure physical fidelity.

Table 1: Time Step Selection Guidelines for Different System Types

System Characteristics	Recommended Time Step	Integration Method	Constraint Algorithm	Typical Applications
All-atom, explicit solvent	1-2 fs	Velocity Verlet	None	Standard protein simulations
All-atom with H-constraints	2 fs	Velocity Verlet	LINCS/SHAKE	Most biomolecular systems
All-atom, optimized	3-4 fs	Velocity Verlet	LINCS/SHAKE	Well-equilibrated systems
Coarse-grained	10-50 fs	Various	N/A	Large-scale dynamics
ML-enhanced	50-200 fs	Learned symplectic map	Learned constraints	Exploratory sampling

Protocol: Time Step Optimization Procedure

• Initial Assessment: Begin with a conservative time step (1 fs) for system equilibration. Monitor energy conservation and stability over 10,000 steps.

• Progressive Increase: Incrementally increase the time step by 0.5 fs intervals, running short simulations (1,000-5,000 steps) at each value. Calculate the fluctuation in total energy for each run.

• Stability Check: Identify the maximum time step where energy drift remains below 0.1% per picosecond and structural parameters (e.g., RMSD) remain stable.

• Constraint Application: Implement bond constraints for hydrogen atoms using LINCS or SHAKE algorithms, allowing further increase to 2 fs.

• Validation: Perform a production simulation of at least 100 ps at the selected time step and verify physical properties match expectations from literature or experimental data.

Hardware Considerations for MD Simulations

CPU and GPU Selection Strategies

MD simulations benefit from different hardware configurations depending on the software package and system size. For CPU-bound workloads, clock speed is often more critical than core count, as much of the simulation workflow involves sequential operations [57]. Mid-tier workstation CPUs with balanced base and boost clock speeds, such as the AMD Threadripper PRO series, typically provide the best performance for the cost. Dual CPU setups with data center processors (AMD EPYC, Intel Xeon Scalable) are recommended only for workloads requiring exceptionally high core counts [57].

GPU acceleration has become essential for high-throughput MD simulations. NVIDIA GPUs currently dominate due to extensive software optimization in packages like AMBER, GROMACS, and NAMD [30] [57]. The precision requirements of the simulation code determine the optimal GPU architecture:

• Mixed Precision Codes: Consumer GPUs (e.g., RTX 4090/5090) provide excellent price/performance ratios for codes like GROMACS that use mixed precision [30].
• Double Precision Codes: Data-center GPUs (NVIDIA A100/H100) are necessary for codes requiring full double-precision (FP64) throughout the calculation, such as CP2K, Quantum ESPRESSO, and VASP [30].

Table 2: Hardware Recommendations for Popular MD Software

Software	Recommended GPU	VRAM Requirements	CPU Priority	Precision Mode
GROMACS	NVIDIA RTX 4090	24 GB for most systems	Clock speed	Mixed precision
AMBER	NVIDIA RTX 6000 Ada	48 GB for large systems	Balanced clock/core count	Mixed precision
NAMD	NVIDIA RTX 4090/6000 Ada	24-48 GB depending on system size	Clock speed	Mixed precision
LAMMPS	NVIDIA RTX 4090	24 GB for most systems	Clock speed	Mixed precision
CP2K	NVIDIA A100/H100	40-80 GB	Core count for parallelism	Double precision

Multi-GPU and Cluster Configurations

For large-scale simulations, multi-GPU configurations can dramatically enhance computational efficiency. AMBER, GROMACS, and NAMD all support multi-GPU execution, enabling researchers to handle larger molecular systems or conduct multiple simultaneous runs [57]. The key advantages include increased throughput, enhanced scalability, and improved resource utilization. When designing multi-GPU systems, consider:

• Node Configuration: Purpose-built workstations and servers with optimized cooling and power delivery ensure stability during extended simulations [57].
• Interconnect Technology: High-speed interconnects (NVLink, InfiniBand) minimize communication overhead between GPUs and nodes.
• Memory Architecture: Systems with large VRAM capacity (e.g., 48 GB per GPU) enable simulation of massive molecular systems exceeding one million atoms.

Protocol: Hardware Selection and Benchmarking

• Precision Requirement Analysis: Determine if your MD code requires full double precision (FP64) or operates efficiently in mixed precision by consulting software documentation [30].

• System Size Assessment: Calculate the approximate memory requirements based on atom count, with typical biomolecular systems requiring 1-2 GB per 100,000 atoms.

• GPU Selection: Choose appropriate GPU hardware based on precision needs and memory requirements from Table 2.

• Benchmark Execution: Run a small, representative simulation (10,000-100,000 steps) on candidate hardware and measure performance in ns/day.

• Cost Evaluation: Calculate computational cost using metrics such as €/ns/day for molecular dynamics or €/10k ligands screened for docking studies [30].

Parallelization Strategies in MD Simulations

Parallelization Architectures and Domain Decomposition

Efficient parallelization is essential for leveraging modern high-performance computing resources. GROMACS employs several parallelization schemes that can be combined hierarchically [63]:

• SIMD (Single Instruction Multiple Data): Utilizes vector processing units in CPUs for parallel execution of floating-point operations on multiple data elements [63].
• OpenMP Multithreading: Shares compute workload across multiple cores within a single node, with lower overhead than MPI for small systems [64] [63].
• MPI (Message Passing Interface): Enables distributed computing across multiple nodes, essential for large-scale simulations [64] [63].
• GPU Offloading: Accelerates computationally intensive tasks like non-bonded force calculations [63].

Domain decomposition is the foundational algorithm for spatial parallelism in MD simulations [61]. The simulation box is divided into domains assigned to different MPI ranks, with each rank calculating forces for particles in its domain. The eighth-shell method minimizes communication overhead by precisely determining which coordinates need to be exchanged between neighboring domains [61]. Dynamic load balancing automatically adjusts domain boundaries during simulation to compensate for inhomogeneous particle distribution or computational load, typically improving performance when force calculation imbalance exceeds 2% [61].

PME Parallelization and Multi-Node Strategies

Particle Mesh Ewald (PME) electrostatics calculations present particular parallelization challenges due to their global communication requirements. The Multiple-Program, Multiple-Data approach addresses this by dedicating a subset of ranks exclusively to PME calculations while others handle particle-particle interactions [61]. This separation improves scalability, with optimal performance typically achieved when 25-50% of ranks are dedicated to PME [61].

For multi-node calculations, pure MPI parallelization is generally recommended, while single-node simulations often achieve best performance with pure OpenMP or hybrid approaches [64]. The GROMACS documentation specifically advises setting the OMP_NUM_THREADS environment variable to 1 for multi-node MPI calculations and to the number of physical cores for single-node OpenMP simulations [64].

Protocol: Parallelization Configuration and Optimization

• Hardware Assessment: Identify the number of nodes, sockets per node, cores per socket, and available GPUs.

• Single-Node Configuration: For local workstations, use pure OpenMP by setting NSCM=1 and OMP_NUM_THREADS to the number of physical cores [64].

• Multi-Node Configuration: For cluster deployments, use pure MPI with OMP_NUM_THREADS=1 and appropriate MPI process distribution [64].

• Domain Decomposition Setup: Configure the domain decomposition grid dimensions to minimize communication volume while maintaining load balance.

• PME Tuning: Adjust the ratio of PP to PME ranks, typically starting with a 3:1 or 4:1 ratio for optimal electrostatics performance [61].

• Performance Monitoring: Run short simulations and examine log files for load imbalance statistics, adjusting decomposition parameters if imbalance exceeds 5%.

Table 3: Key Research Reagent Solutions for Molecular Dynamics Simulations

Item	Function	Examples/Alternatives	Application Context
MD Software Suite	Primary simulation engine	GROMACS, AMBER, NAMD, LAMMPS	All simulation types
Force Field	Defines interatomic potentials	CHARMM, AMBER, OPLS, Martini	System-dependent selection
Visualization Tool	Trajectory analysis and rendering	VMD, PyMol, ChimeraX	Result interpretation
HPC Environment	Execution infrastructure	Local clusters, cloud computing	Variable access models
Enhanced Sampling	Accelerate rare events	Metadynamics, Umbrella Sampling	Complex barrier crossing

Integrated Optimization Workflow

The optimization of MD simulation performance requires careful consideration of the interplay between time step selection, hardware capabilities, and parallelization strategies. The following diagram illustrates the decision process for configuring an optimal MD simulation:

This integrated approach ensures that all aspects of simulation performance are addressed systematically. Researchers should iterate through the optimization process, making incremental adjustments to each parameter while monitoring both performance metrics and physical accuracy.

Inadequate conformational sampling remains a fundamental challenge in molecular dynamics (MD) simulations, often limiting their ability to reveal biologically relevant protein states and functional mechanisms. This application note details modern enhanced sampling strategies to overcome the limitations of conventional MD. We provide a comprehensive overview of advanced methods, including true reaction coordinate-driven sampling, machine learning-enhanced techniques, and various collective variable-based approaches, framed within a protocol for assessing and addressing sampling deficiencies. Quantitative comparisons of method performance, detailed experimental protocols for implementation, and a curated toolkit of research reagents are included to enable researchers to select and apply these strategies effectively in drug discovery and basic research.

Molecular Dynamics simulations have emerged as a crucial methodology for studying biological systems at the atomic level, yet insufficient sampling often restricts their application [65]. The core challenge stems from the rough energy landscapes of biomolecules, characterized by numerous local minima separated by high-energy barriers that govern biomolecular motion [65]. This energy landscape roughness means that conventional MD simulations frequently fail to reach all relevant conformational substates connected with biological function within practical computational timeframes [65]. Recent studies demonstrate that proteins can remain trapped in non-relevant conformations for extended periods without returning to functionally significant states [65].

The time scale gap between MD simulations (microseconds) and functionally important biological processes (milliseconds to hours) makes enhanced sampling methods essential for studying protein function [66]. Large conformational changes are often critical for protein activity, particularly in catalysis where large amplitude movements are frequently required, or in membrane transport where channels and transporters undergo significant conformational changes during gating processes [65]. These complex processes typically exceed the capabilities of straightforward MD simulations, necessitating the implementation of enhanced sampling algorithms [65].

Enhanced Sampling Methodologies

Collective Variable-Based Methods

Collective variable (CV)-based methods enhance sampling by applying bias potentials along carefully selected degrees of freedom believed to characterize the slow dynamics of the system.

Metadynamics operates by discouraging the re-sampling of previously visited states, effectively "filling the free energy wells with computational sand" [65]. This approach directs computational resources toward broader exploration of the free-energy landscape [65]. The method does not depend on a highly accurate description of the potential energy surface, as misevaluated conformations can be recalculated and errors tend to "even out" over time [65]. However, metadynamics does require a low-dimensional system description using a small set of collective coordinates to produce an accurate free energy surface description [65]. Metadynamics has been successfully applied to diverse biological problems including protein folding, molecular docking, phase transitions, and conformational changes [65].

Umbrella Sampling employs harmonic restraints along a reaction coordinate to enhance sampling in high-free energy regions. The method is particularly effective for calculating free energy differences and potential of mean force along defined coordinates [45]. Adaptive Biasing Force (ABF) method is another directed dynamics approach that derives from similar principles as metadynamics, gradually removing the free energy energy barrier along a specified collective variable [65].

Temperature-Based and Generalized Ensemble Methods

Replica-Exchange Molecular Dynamics (REMD), also known as parallel tempering, employs independent parallel simulations at different temperatures, with periodic exchanges of system states between temperatures based on the Metropolis criterion [65] [67]. This generalized-ensemble algorithm enables efficient random walks in both temperature and potential energy spaces [65]. The effectiveness of temperature-based REMD (T-REMD) is strongly dependent on the activation enthalpy and the choice of maximum temperature [65]. Variants include Hamiltonian REMD (H-REMD) for enhanced sampling in dimensions other than temperature, multiplexed REMD (M-REMD) with multiple replicas per temperature level, and constant pH REMD for studying protein protonation states [65].

Simulated Annealing methods draw inspiration from metallurgical annealing processes, where an artificial temperature decreases during the simulation to guide the system toward low-energy states [65]. Variants include classical simulated annealing (CSA), fast simulated annealing (FSA), and generalized simulated annealing (GSA), the latter being applicable to large macromolecular complexes at relatively low computational cost [65].

Advanced and Machine Learning-Enhanced Approaches

True Reaction Coordinate (tRC) methods address the fundamental challenge of identifying the few essential protein coordinates that fully determine the committor (probability of reaching a product state) [66]. These coordinates are recognized as optimal collective variables for accelerating conformational changes, as they control both conformational changes and energy relaxation [66]. Biasing true reaction coordinates has been shown to accelerate conformational changes and ligand dissociation in systems like the PDZ2 domain and HIV-1 protease by 10⁵ to 10¹⁵-fold, with resulting trajectories following natural transition pathways [66].

Machine Learning-Enhanced Sampling represents the cutting edge, with approaches using neural network potentials to approximate free energy surfaces and their gradients [45]. ML algorithms can identify meaningful collective variables that correlate with high variance or slow degrees of freedom using deep neural networks [45]. Platforms like PySAGES provide integration of ML frameworks with MD software libraries, enabling enhanced-sampling MD simulations on GPUs with methods including artificial neural network sampling and adaptive biasing force using neural networks [45].

Table 1: Quantitative Comparison of Enhanced Sampling Methods

Method	Acceleration Mechanism	Typical Acceleration Factor	System Size Suitability	Key Applications
Metadynamics [65]	Fills free energy wells with bias potential	Varies by system	Small to medium systems	Protein folding, molecular docking, conformational changes
REMD [65]	Temperature exchanges overcome barriers	More efficient than MD with positive activation energy [65]	Medium to large systems	Peptide and protein folding, free energy landscapes
True Reaction Coordinates [66]	Bias applied to essential coordinates	10⁵ to 10¹⁵ for specific systems	All sizes	Natural transition pathways, ligand dissociation
Weighted Ensemble [68]	Parallel resampling based on progress coordinates	Enables rare event sampling	Small to medium systems	Conformational space exploration, rare events
Simulated Annealing [65]	Gradual temperature decrease	Efficient for large complexes	Large macromolecular complexes	Structure refinement, global minimum search

Quantitative Assessment of Sampling Quality

Effective Sample Size (ESS) provides a crucial metric for quantifying sampling quality by estimating the number of statistically independent configurations contained in a simulated ensemble [69]. The ESS can be estimated from variances in state populations using the formula:

[ Nj^{eff} = \frac{\bar{p}j(1-\bar{p}j)}{\sigmaj^2} ]

where (\bar{p}j) is the observed average population in region j, and (\sigmaj^2) is its variance [69]. This approach quantifies sampling quality based on the fundamental observables of state populations, which inherently reflect the slow timescales of the system [69].

Automated State Identification enables practical assessment of sampling quality through a hierarchical procedure that groups configuration-space regions based on transition rates [69]. Regions with high mutual transition rates are grouped into the same physical state, with the procedure highlighting the hierarchical nature of the energy landscape [69].

Table 2: Sampling Assessment Metrics and Tools

Metric/Tool	Description	Implementation
Effective Sample Size (ESS) [69]	Estimates statistically independent configurations	Variance analysis of state populations
State Population Variances [69]	Fundamental slow observables for assessing convergence	Requires multiple simulation replicates
Automated State Approximation [69]	Groups regions by transition rates	Analysis of dynamics trajectories
Weighted Ensemble Benchmarking [68]	Standardized assessment using progress coordinates	WESTPA with TICA analysis
Structural Histogram Analysis [69]	Bin populations across configuration space	Alternative to state-based analysis

Experimental Protocols

Protocol 1: True Reaction Coordinate Identification and Biasing

Objective: Identify and bias true reaction coordinates to accelerate conformational sampling of protein functional processes.

Materials: Single protein structure, MD simulation software with enhanced sampling capabilities (e.g., PySAGES, PLUMED, SSAGES), high-performance computing resources with GPU acceleration.

Methodology:

• Potential Energy Flow Calculation: Compute potential energy flows (PEFs) through individual coordinates using the equation: [ \Delta Wi(t1,t2) = -\int{qi(t1)}^{qi(t2)} \frac{\partial U(\mathbf{q})}{\partial qi} dqi ] where (dWi) represents the energy cost of motion of coordinate (qi) [66].

• Singular Coordinate Generation: Apply the generalized work functional (GWF) method to generate an orthonormal coordinate system (singular coordinates) that disentangles true reaction coordinates from non-essential coordinates by maximizing PEFs through individual coordinates [66].

• True Reaction Coordinate Identification: Identify true reaction coordinates as the singular coordinates with the highest potential energy flows [66].

• Biasing and Sampling: Apply bias potentials to the identified true reaction coordinates to enhance sampling, achieving acceleration factors of 10⁵ to 10¹⁵ for specific systems like HIV-1 protease [66].

• Trajectory Analysis: Generate natural reactive trajectories that follow physical transition pathways and pass through transition state conformations [66].

Protocol 2: Machine Learning-Enhanced Sampling with PySAGES

Objective: Implement ML-enhanced sampling using GPU-accelerated tools for efficient free energy calculation.

Materials: PySAGES library, compatible MD backend (HOOMD-blue, OpenMM, LAMMPS, JAX MD, ASE), GPU-enabled computing resources.

Methodology:

• System Setup: Wrap traditional backend scripting code into simulation generator functions following PySAGES requirements [45].

• Collective Variable Selection: Define differentiable functions of atomic coordinates for collective variables, automatically differentiated via JAX's grad transform for biasing force estimation [45].

• Sampling Method Configuration: Initialize specialized routines for selected sampling methods (options include Umbrella Sampling, Metadynamics, Adaptive Biasing Force, Artificial Neural Network Sampling, and others) [45].

• Simulation Execution: Run simulations with PySAGES managing the snapshot object for backend-agnostic access to particle positions, velocities, and forces using DLPack for C++-based MD libraries [45].

• Free Energy Calculation: Utilize PySAGES' analyze interface for post-simulation analysis and automatic free energy calculation based on the chosen sampling method [45].

Protocol 3: Sampling Assessment with Effective Sample Size

Objective: Quantify sampling quality using effective sample size estimation from state populations.

Materials: Multiple MD trajectories of the same system, analysis tools for state identification and population variance calculation.

Methodology:

• Trajectory Generation: Perform multiple independent simulations (Nobs) from different initial conditions [69].

• State Approximation: Apply automated procedure to identify approximate physical states by analyzing transition rates between configuration-space regions, grouping regions with high mutual transition rates [69].

• Population Calculation: For each trajectory i, calculate the population (p_j^{(i)}) for each state j [69].

• Variance Analysis: Compute average state populations and variances: [ \bar{p}j = \frac{1}{N{obs}}\sumi^{N{obs}} pj^{(i)}, \quad \sigmaj^2 = \frac{1}{N{obs}}\sumi^{N{obs}} (pj^{(i)} - \bar{p}_j)^2 ] [69].

• ESS Estimation: Calculate effective sample size for each state: [ Nj^{eff} = \frac{\bar{p}j(1-\bar{p}j)}{\sigmaj^2} ] [69].

• Sampling Quality Assessment: Use the ESS to determine whether additional sampling is required, with higher ESS values indicating better convergence [69].

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Software Tools for Enhanced Sampling

Tool/Platform	Function	Key Features	Compatibility
PySAGES [45]	Advanced sampling library	GPU acceleration, JAX differentiation, multiple backend support	HOOMD-blue, OpenMM, LAMMPS, JAX MD, ASE
PLUMED [67]	Enhanced sampling plugin	Extensive method library, community support	GROMACS, AMBER, NAMD, LAMMPS
SSAGES [45]	Advanced sampling suite	Multiple method implementations, cross-platform	Various MD engines
WESTPA [68]	Weighted ensemble sampling	Rare event sampling, progress coordinate-based	Custom interfaces
OpenMM [68]	MD simulation toolkit	GPU acceleration, Python API	Standalone or with plugins

Workflow Visualization

Diagram 1: Enhanced Sampling Implementation Workflow

Addressing inadequate conformational coverage requires a systematic approach to enhanced sampling, combining rigorous assessment of existing sampling quality with targeted application of advanced methods. The strategies outlined in this application note—from true reaction coordinate identification to machine learning-enhanced sampling—provide researchers with a comprehensive toolkit for overcoming the fundamental time-scale limitations of conventional molecular dynamics. By implementing these protocols and utilizing the accompanying assessment metrics, researchers can significantly improve their ability to sample biologically relevant conformational states, ultimately advancing drug discovery and fundamental understanding of protein function.

Molecular dynamics (MD) simulations have become an indispensable tool in structural biology and computer-aided drug discovery, providing atomic-level insight into the dynamic behavior of proteins and other biomolecules [1]. The accuracy of these simulations, however, is fundamentally governed by the quality of the molecular mechanics force fields that describe interatomic interactions [70]. While substantial progress has been made in force field development, significant challenges remain in accurately modeling environment-dependent properties, particularly protonation states, which are crucial for simulating pH-mediated biological processes and proton-coupled conformational changes [71].

Protonation equilibria of protein sidechains are shifted by complex electrostatic interactions and desolvation effects within the protein environment [71]. Standard fixed-charge force fields often struggle to capture these subtle yet critical effects, potentially leading to inaccurate predictions of protein dynamics, ligand binding, and ultimately, drug efficacy [72] [71]. This application note examines the limitations of current force fields in handling protonation states and environment-dependent parameters, provides protocols for assessing and mitigating these limitations, and presents emerging solutions that leverage advanced sampling techniques and machine learning approaches to achieve more accurate and biologically relevant simulations.

Force Field Limitations in Modeling Protonation States

Key Challenges and Systematic Errors

Recent investigations into all-atom constant pH molecular dynamics simulations have revealed significant force field dependencies in calculating pKa values of titratable residues. A 2024 study specifically examined this phenomenon using the mini-protein BBL as a benchmark system [71].

Table 1: Force Field Performance in pKa Calculations for BBL Protein

Force Field	Water Model	Key Limitations	Buried Histidine Error	Salt-Bridge Glu Error
Amber ff19sb	OPC	Undersolvation of neutral histidines; Overstabilized salt bridges	Significant overestimated pKa downshift	Large overestimated pKa downshifts
Amber ff14sb	TIP3P	Same as above but more pronounced	Larger error magnitude	Larger error magnitude
CHARMM c22/CMAP	CHARMM TIP3P	Similar issues but different error magnitude	Significant pKa error	Significant pKa error

The study demonstrated that all tested force fields exhibited substantial errors in calculating pKa values for buried residues and those involved in salt-bridge interactions, though with varying magnitudes [71]. The most significant errors were observed for:

• Buried Histidines: All force fields showed significantly overestimated pKa downshifts due to undersolvation of neutral histidines [71].
• Salt-Bridge Interactions: Glutamic acids involved in salt-bridge interactions exhibited overestimated pKa downshifts due to overstabilization of these electrostatic interactions [71].

Notably, the investigation found that ff19sb with OPC water demonstrated significantly better accuracy compared to ff14sb with TIP3P water, highlighting the critical importance of both protein force field and water model selection [71].

Physical Origins of Force Field Deficiencies

The inaccuracies in modeling protonation states stem from several physical approximations inherent in standard force fields:

• Electrostatic Treatment: Fixed partial atomic charges cannot adapt to changes in local dielectric environment or protonation state [71].
• Solvation Effects: Implicit and explicit solvent models have limitations in capturing the complex thermodynamics of proton binding and release [72].
• Polarization Neglect: Standard force fields do not account for electronic polarization effects that occur when the charge distribution of a molecule responds to its environment [47].

These limitations are particularly problematic for drug discovery applications, where accurate prediction of binding affinities requires precise modeling of electrostatic contributions and protonation state changes upon ligand binding [72] [73].

Experimental Protocols for Force Field Validation

Constant pH MD Simulation Protocol

The following protocol, adapted from recent benchmark studies [71], provides a methodology for assessing force field performance in modeling protonation equilibria:

Table 2: Key Research Reagents and Computational Tools

Reagent/Tool	Function/Application	Key Features
AMBER2024	Molecular dynamics software	Includes PME-CpHMD implementation
CHARMM	Molecular dynamics software	Alternative MD engine with CpHMD capabilities
BBL Mini-protein	Benchmark system	Contains buried His and salt-bridge Glu residues
Amber ff19sb	Protein force field	Latest Amber force field with OPC water compatibility
OPC Water Model	Explicit solvent	Optimized for accurate electrostatic properties
NBFIX	Parameter correction	Atom-pair specific Lennard-Jones corrections

System Preparation:

• Obtain protein coordinates from PDB (e.g., BBL: 1W4H) and select the first NMR model [71].
• Add terminal capping groups (ACE at N-terminus, NH2 at C-terminus) to eliminate confounding electrostatic effects from terminal charges [71].
• Build hydrogen positions using standard algorithms (e.g., HBUILD in CHARMM), adding dummy hydrogens to syn positions of carboxylate oxygens on Asp and Glu sidechains [71].
• Solvate the protein in a truncated octahedral water box with minimum 15 Ã… distance between protein heavy atoms and box edges [71].
• Add ions to neutralize system charge and achieve desired ionic strength (e.g., 150 mM NaCl) [71].

Simulation Parameters:

• Employ the particle mesh Ewald method for long-range electrostatics with a 1.0 Ã… grid spacing [71].
• Use the SHAKE algorithm to constrain bonds involving hydrogen atoms [71].
• Maintain constant temperature (300 K) and pressure (1 atm) using appropriate thermostats and barostats [71].
• Utilize a 2-fs time step for production simulations [71].

pH Replica-Exchange Protocol:

• Set up 16 pH replicas spanning the pH range of interest (e.g., pH 1.0-8.5 with 0.5 unit increments) [71].
• Perform asynchronous replica exchange every 1000 MD steps (2 ps) according to the Metropolis criterion [71].
• Run production simulations for sufficient time to ensure pKa convergence (typically 20-40 ns per replica) [71].
• Discard initial equilibration period (typically 10 ns per replica) from analysis [71].

Figure 1: Constant pH MD Simulation Workflow

Binding Free Energy Calculation Protocol

Accurate prediction of binding free energies is crucial for drug discovery and provides another important validation metric for force field performance:

MM/GBSA Protocol:

• Run multiple independent MD simulations of the protein-ligand complex, apo protein, and free ligand [72].
• Extract snapshots at regular intervals from equilibrated portions of trajectories [72].
• Calculate molecular mechanics energies, solvation energies (GB/SA), and entropy terms for each snapshot [72].
• Compute binding free energies using the MM/GBSA or MM/PBSA approach and average across snapshots [72].

Alchemical Free Energy Perturbation:

• Use thermodynamic integration or free energy perturbation methods to gradually eliminate nonbonded interactions between ligand and environment [72].
• Employ machine learning approaches to reduce the number of required calculations when screening large chemical libraries [72].
• Leverage AlphaFold-predicted protein models as starting structures when experimental structures are unavailable [72].

Emerging Solutions and Methodological Advances

Force Field Improvements and Corrections

Recent research has identified several promising approaches for addressing current limitations:

• Water Model Selection: Using more accurate water models like OPC instead of TIP3P can significantly improve pKa prediction accuracy [71].
• NBFIX Corrections: Applying atom-pair specific Lennard-Jones corrections can partially alleviate salt-bridge related pKa errors, though complete resolution remains challenging [71].
• Polarizable Force Fields: Next-generation force fields that explicitly account for electronic polarization show promise for better modeling of environment-dependent effects [47].
• Machine Learning Potentials: ML-driven approaches such as AIMNet2 offer quantum-mechanical accuracy at dramatically reduced computational cost, enabling more accurate refinement of protein structures [74].

Machine Learning Accelerated Quantum Refinement

The recently developed AQuaRef method represents a significant advancement in force field refinement [74]:

Figure 2: Machine Learning Quantum Refinement Workflow

This approach leverages machine-learned interatomic potentials trained on quantum mechanical data to refine protein structures against experimental data, offering several advantages:

• Superior Geometric Quality: Structures refined with AQuaRef show systematically better geometry compared to standard techniques [74].
• Proton Position Determination: The method aids in determining challenging proton positions, such as short hydrogen bonds [74].
• Computational Efficiency: The MLIP approach scales linearly with system size, making it practical for large proteins [74].

Accurate handling of protonation states and environment-dependent parameters remains a significant challenge in force field development, with important implications for drug discovery applications. Recent studies have quantitatively documented the limitations of current force fields in modeling pKa shifts and electrostatic interactions, particularly for buried residues and those involved in salt bridges [71].

The most promising paths forward include the development of polarizable force fields, the integration of machine learning potentials to capture quantum mechanical effects at manageable computational cost [74], and the continued refinement of explicit solvent models and parameter optimization strategies. As these methods mature and become more widely adopted, they will enhance the predictive power of MD simulations in drug discovery, enabling more reliable prediction of binding affinities and accelerating the development of novel therapeutics.

For researchers employing MD simulations in structure-based drug design, the recommended strategy is to: 1) Validate force field performance on systems with known experimental pKa values when possible, 2) Utilize constant pH MD methods to account for protonation state changes, 3) Consider emerging ML-based refinement tools to improve structural models, and 4) Employ multiple force fields and water models to assess the robustness of findings.

These approaches will help mitigate current force field limitations while the field continues to develop more accurate and physically realistic models of biomolecular interactions.

Validating Results and Comparing Methodologies for Robust Scientific Insight

Molecular dynamics (MD) simulations serve as "virtual molecular microscopes," providing atomistic details into the dynamic nature of proteins that often remain hidden from traditional biophysical techniques [75]. The predictive capability of MD is constrained by two fundamental challenges: the sampling problem, where simulations may need to be impractically long to accurately describe certain dynamical properties, and the accuracy problem, where insufficient mathematical descriptions of physical and chemical forces can yield biologically meaningless results [75]. compelling measure of a force field's accuracy is its ability to recapitulate and predict experimental observables, though significant challenges exist in this validation process as experimental data typically represent averages over space and time, potentially obscuring the underlying distributions and timescales [75]. This application note establishes detailed protocols for benchmarking MD simulations against experimental data, framed within the broader context of molecular dynamics simulation protocol research.

Experimental Observables for MD Validation

Key Biophysical Techniques for Correlation

Multiple experimental techniques provide measurable observables that can be directly compared to MD simulation outputs. The correspondence between simulation and experiment does not necessarily constitute a full validation of the conformational ensemble, as multiple diverse ensembles may produce averages consistent with experiment [75]. The following table summarizes primary experimental metrics used for MD validation:

Table 1: Experimental Observables for MD Validation

Experimental Technique	Measurable Observable	Structural & Dynamic Information	Comparison Method
X-ray Crystallography	Atomic coordinates, B-factors	Static structure, flexibility	Root-mean-square deviation (RMSD), B-factor correlation [75]
NMR Spectroscopy	Chemical shifts, relaxation parameters	Local environment, dynamics on multiple timescales	Chemical shift prediction and correlation [75] [76]
Cryo-EM	Density maps	Large-scale conformations	Density fitting and flexibility analysis
FRET	Distance distributions	Inter-domain distances and dynamics	Distance distribution comparison [76]
HDX-MS	Hydrogen-deuterium exchange	Solvent accessibility and dynamics	Exchange rate calculation from trajectories

Dynamic Cross-Correlation Analysis

Beyond static structural comparisons, MD simulations enable the identification of dynamic cross-correlation networks through covariance analysis of atomic fluctuations [76]. The cross-correlation coefficient C(i,j), which quantifies the extent of correlated motion between atoms i and j, is calculated as:

[ C{ij} = \frac{\langle \Delta ri \cdot \Delta rj \rangle}{\langle \Delta ri^2 \rangle^{1/2} \langle \Delta r_j^2 \rangle^{1/2}} ]

where (\Delta r_i) is the displacement vector of atom i and the angle brackets denote an ensemble average [76]. Positive values (up to 1) indicate correlated motions in the same direction, while negative values (down to -1) indicate anti-correlated motions in opposite directions [76]. These correlation networks are critical for understanding allosteric regulation and can inform enzyme engineering strategies by identifying mutation targets distant from active sites whose dynamics correlate with functional regions [76].

Comprehensive Benchmarking Protocol

System Preparation and Simulation Parameters

This protocol utilizes the well-characterized Engrailed homeodomain (EnHD) and Ribonuclease H (RNase H) as model systems, following established benchmarking approaches [75]. The initial coordinates for EnHD were obtained from PDB ID: 1ENH, while RNase H coordinates came from PDB ID: 2RN2 [75]. Crystallographic solvent atoms were removed prior to simulation setup.

Table 2: Simulation Package and Force Field Combinations for Benchmarking

Software Package	Force Field	Water Model	Integration Algorithm	Nonbonded Treatment
AMBER14	AMBER ff99SB-ILDN [75]	TIP4P-EW [75]	Particle Mesh Ewald
GROMACS	AMBER ff99SB-ILDN [75]
NAMD	CHARMM36 [75]
ilmm	Levitt et al. [75]

All simulations should be performed in triplicate for a minimum of 200 nanoseconds each using periodic boundary conditions and explicit water molecules [75]. Simulation temperature should match experimental conditions (298K for EnHD at pH 7.0; 298K for RNase H at pH 5.5 with protonated histidine residues) [75].

Workflow for Comparative Analysis

The following diagram illustrates the complete benchmarking workflow from system preparation through quantitative comparison:

Force Field and Sampling Considerations

When benchmarking simulations, it is crucial to recognize that differences in simulated protein behavior arise not only from force fields but also from numerous other factors including water models, algorithms that constrain motion, handling of atomic interactions, and the simulation ensemble employed [75]. Studies have demonstrated that while multiple force fields may reproduce a variety of experimental observables equally well at room temperature, they can show significant divergence when sampling larger amplitude motions such as thermal unfolding [75]. Some packages may fail to allow the protein to unfold at high temperature or provide results at odds with experiment despite reasonable performance under native conditions [75].

Quantitative Benchmarking Metrics and Analysis

Statistical Measures for Agreement Assessment

The following quantitative metrics provide rigorous assessment of simulation-experiment agreement across multiple observables:

Table 3: Quantitative Metrics for Simulation-Experiment Agreement

Metric Category	Specific Metric	Calculation	Acceptance Threshold
Structural Accuracy	Root-mean-square deviation (RMSD)	(\sqrt{\frac{1}{N}\sum{i=1}^N |ri^{sim} - r_i^{exp}|^2})	< 2.0 Ã… (backbone)
Flexibility Correlation	B-factor correlation coefficient	Pearson r of Cα B-factors	r > 0.6
NMR Validation	Chemical shift correlation	Pearson r of backbone chemical shifts	r > 0.8
Ensemble Sampling	Radius of gyration distribution	Kolmogorov-Smirnov test vs. SAXS	p > 0.05
Dynamic Cross-correlation	Covariance matrix similarity	Matrix correlation of DCCM	Situation-dependent

Cross-Correlation Network Analysis Protocol

For dynamic cross-correlation analysis using GROMACS and Bio3D [76]:

• Trajectory Preparation: Ensure trajectories are properly aligned and centered to remove global rotation and translation.
• Covariance Calculation: Calculate the covariance matrix using GROMACS g_covar or directly within Bio3D.
• Cross-Correlation Computation: Compute the normalized cross-correlation matrix using the Bio3D R package.
• Network Visualization: Generate dynamical cross-correlation matrix (DCCM) plots and network representations.
• Community Detection: Identify communities of highly correlated residues using clustering algorithms.

The following diagram illustrates the dynamic cross-correlation network identification process:

Research Reagent Solutions

Table 4: Essential Research Reagents and Computational Tools

Category	Specific Tool/Reagent	Function/Purpose	Application Notes
MD Software	GROMACS [76]	Molecular dynamics simulation package	Fast, free, user-friendly; continually upgraded and maintained
MD Software	AMBER [75]	Molecular dynamics simulation package
MD Software	NAMD [75]	Molecular dynamics simulation package
Analysis Tool	Bio3D R Package [76]	Analysis of biomolecular structure and dynamics	Calculates dynamic cross-correlation matrices from trajectories
Force Field	AMBER ff99SB-ILDN [75]	Protein force field
Force Field	CHARMM36 [75]	Protein force field
Water Model	TIP4P-EW [75]	Extended simple point charge water model	Used with AMBER ff99SB-ILDN force field
Protein System	Engrailed homeodomain (EnHD) [75]	Benchmark protein	54 residues, three α-helices; PDB ID: 1ENH
Protein System	RNase H [75]	Benchmark protein	155 residues, α/β protein; PDB ID: 2RN2

Robust benchmarking of MD simulations against experimental data requires careful attention to simulation protocols, force field selection, and comprehensive comparison metrics. Researchers should implement multiple replicate simulations to enhance conformational sampling and compare results across different software package and force field combinations to identify potential systematic biases [75]. The dynamic cross-correlation analysis protocol provides particularly valuable insights for enzyme engineering applications, identifying allosteric networks and potential mutation targets distant from active sites [76]. By adopting these standardized benchmarking approaches, researchers can increase confidence in their simulation results and generate more reliable predictions for drug development applications.

Molecular dynamics (MD) simulations have emerged as a powerful tool in biomedical research, offering unparalleled insights into intricate biomolecular processes such as structural flexibility, molecular interactions, and conformational changes [56]. These simulations play a pivotal role in therapeutic approaches and drug development by enabling researchers to study biological systems at an atomic level, from small proteins in vacuum to large protein complexes in solvated environments [77]. However, the accuracy and biological relevance of MD simulations depend critically on the proper implementation of thermodynamic control algorithms and enhanced sampling techniques. Without these, simulations may fail to capture essential physiological conditions or adequately sample the conformational space necessary to understand biological function [78] [77].

The fundamental challenge in MD simulations lies in their two inherent limitations: potential inaccuracies in force fields and the high computational cost required for adequate sampling [77]. Biological molecules exhibit rough energy landscapes with many local minima separated by high-energy barriers, making it easy for simulations to become trapped in non-functional states that fail to represent the full spectrum of biologically relevant conformations [77] [65]. This review provides a comprehensive comparative analysis of the computational algorithms that address these challenges—thermostats for temperature control, barostats for pressure regulation, and enhanced sampling methods for accelerating the exploration of conformational space—all within the context of molecular dynamics simulation protocol research for drug development applications.

Thermostats: Temperature Control Algorithms

Theoretical Foundations of Temperature Control

In molecular dynamics, temperature is defined by the average kinetic energy of all particles in the system [78]. At the molecular level, a system in equilibrium exhibits a distribution of particle velocities described by the Maxwell-Boltzmann distribution [78] [79]:

[fv(v)=\left(\frac{m}{2\pi kB T}\right)^{3/2}\cdot4\pi v^2\cdot\exp({-mv^2/2k_B T})]

where (m) represents particle mass, (k_B) is Boltzmann's constant, (T) is temperature, and (v) is velocity [78]. The instantaneous temperature is calculated from the total kinetic energy and the number of degrees of freedom in the system, with the thermodynamic temperature T being the average of this instantaneous value over time [79].

MD simulations typically simulate one of three thermodynamic ensembles: the microcanonical (constant NVE), canonical (constant NVT), or isothermal-isobaric (constant NPT) ensembles [78]. While NVE simulations conserve energy and are relatively straightforward to implement, most biologically relevant simulations require NVT or NPT ensembles to mimic experimental conditions, necessitating the use of temperature control algorithms (thermostats) [78].

Classification and Comparative Analysis of Thermostats

Temperature control algorithms can be categorized into four primary classes: strong coupling methods, weak coupling methods, stochastic methods, and extended system dynamics [78]. The table below provides a comprehensive comparison of these thermostat classes and their specific implementations.

Table 1: Comparative Analysis of Temperature Control Algorithms (Thermostats)

Algorithm Class	Specific Method	Working Principle	Ensemble Accuracy	Advantages	Disadvantages	Typical Applications
Strong Coupling	Velocity Rescaling	Directly rescales velocities to target temperature [78]	Does not produce correct ensemble [78]	Simple implementation	Creates hot spots; non-physical [78]	Heating/cooling; non-equilibrium simulations [78]
Strong Coupling	Velocity Reassignment	Periodically assigns new random velocities [78]	Does not produce correct ensemble [78]	Fast equilibration	Disrupts kinetic-potential energy correlation [78]	System initialization [78]
Weak Coupling	Berendsen	Scales velocities by factor proportional to T difference [78] [79]	Lower variance than true canonical ensemble [78]	Robust, fast convergence [78]	Artificially suppressed fluctuations [78]	System relaxation; equilibration stages [78]
Stochastic	Andersen	Randomizes velocities for subset of atoms based on MB distribution [78]	Correctly samples canonical ensemble [78]	Good sampling quality	Impairs correlated motions; slows kinetics [78]	Systems where kinetics not primary focus [78]
Stochastic	Lowe-Andersen	Momentum-conserving variant of Andersen [78]	Correctly samples canonical ensemble [78]	Better diffusion properties than Andersen	Still perturbs dynamics	When momentum conservation is important [78]
Stochastic	Bussi	Stochastic velocity rescaling with proper random factor [78]	Correctly samples canonical ensemble [78]	Correct fluctuations	More complex implementation	Production simulations requiring correct ensembles [78]
Stochastic	Langevin	Adds frictional and random forces [78]	Correctly samples canonical ensemble [78]	Mimics solvent viscosity	Interferes with natural dynamics	Implicit solvent simulations [78]
Extended System	Nosé-Hoover	Adds artificial variable with "heat bath mass" [78] [79]	Produces correct canonical ensemble [78] [79]	Preserves correlated motions [78]	Temperature oscillations; slow convergence [78]	Production simulations; kinetics studies [78]
Extended System	Nosé-Hoover Chains	Chain of thermostat variables with different masses [78]	Produces correct canonical ensemble [78]	Suppresses oscillations	More parameters to tune	Small systems; requires precise sampling [78]

Implementation Considerations for Thermostats

The selection of an appropriate thermostat depends on the specific stage of simulation and the properties of interest. For initial equilibration, the Berendsen thermostat is particularly useful due to its robust and predictable convergence, despite its inability to produce correct thermodynamic ensembles [78]. For production simulations where accurate sampling of the canonical ensemble is crucial, extended system methods such as Nosé-Hoover or stochastic methods like Bussi velocity rescaling are more appropriate [78].

Local thermostats, which control temperature in selected groups of atoms independently, can address issues of slow heat transfer in heterogeneous systems, though they may cause unrealistic dynamics for small solutes due to significant temperature fluctuations [78]. Most major MD packages, including GROMACS, NAMD, and AMBER, provide implementations of multiple thermostats, allowing researchers to select the most suitable algorithm for their specific system [78].

Barostats: Pressure Control Algorithms

Theoretical Foundations of Pressure Control

Pressure in molecular dynamics represents a force exerted by particle collisions with container walls, described mathematically through the virial equation [80]:

[{P}=\frac{NK{B}T}{V}+\frac{1}{3V}\langle\sum{r{ij}F_{ij}}\rangle]

The first term corresponds to the ideal gas contribution, while the second term accounts for internal forces acting on each atom [80]. Barostats maintain constant pressure by adjusting the volume of the simulation cell, typically by scaling atomic coordinates by a small factor at each step [80].

Classification and Comparative Analysis of Barostats

Pressure control algorithms fall into four main categories: weak coupling methods, extended system methods, stochastic methods, and Monte-Carlo approaches [80]. The following table compares these methods across multiple dimensions.

Table 2: Comparative Analysis of Pressure Control Algorithms (Barostats)

Algorithm Class	Specific Method	Working Principle	Ensemble Accuracy	Advantages	Disadvantages	Typical Applications
Weak Coupling	Berendsen	Scales volume by increment proportional to P difference [80]	Does not sample exact NPT ensemble [80]	Efficient equilibration [80]	Artifacts in inhomogeneous systems [80]	Equilibration stages [80]
Extended System	Parrinello-Rahman	Allows changes in simulation cell shape [80]	Correct ensemble [80]	Studies structural transformations	Volume oscillations [80]	Solids under stress; phase transitions [80]
Extended System	MTTK	Extension of Nosé-Hoover for constant pressure [80]	Correct ensemble [80]	Better for small systems	Complex implementation	Small system NPT simulations [80]
Stochastic	Langevin Piston	Based on MTTK with additional damping/stochastic forces [80]	Correct ensemble [80]	Faster convergence; less oscillation	Introduces randomness	Production simulations [80]
Stochastic	Stochastic Cell Rescaling	Improved Berendsen with stochastic term [80]	Correct NPT fluctuations [80]	Fast convergence without oscillations	Recently developed	All simulation stages [80]
Monte-Carlo	Monte-Carlo Barostat	Random volume changes with MC acceptance probability [80]	Correct ensemble [80]	Does not require virial computation	Pressure not available at runtime	Specialized applications [80]

Practical Implementation of Barostats

The choice of barostat significantly impacts simulation stability and biological relevance. For instance, in studies of bubble nucleation in dielectric fluids, pressure-controlled simulations reveal different nucleation and boiling behaviors compared to fixed-volume models [81]. The Berendsen barostat, while excellent for equilibration, should be avoided in production runs of heterogeneous systems like aqueous biopolymers due to its artificial suppression of pressure fluctuations [80].

For production simulations, the Langevin piston or stochastic cell rescaling methods provide good performance with correct ensemble generation [80]. The Monte-Carlo barostat offers an alternative approach that doesn't require virial computation but provides no pressure information during runtime [80]. When combining thermostats and barostats, the Nosé-Hoover thermostat is frequently paired with the Parrinello-Rahman barostat for consistent sampling of the isothermal-isobaric ensemble [80].

Enhanced Sampling Methods

The Sampling Challenge in Biomolecular Simulations

Biomolecular systems typically exhibit rough energy landscapes with numerous local minima separated by high energy barriers [77] [65]. This landscape roughness often traps conventional MD simulations in non-functional states, preventing adequate sampling of all relevant conformational substates, particularly those connected with biological function [65]. Enhanced sampling techniques address this limitation by facilitating barrier crossing and accelerating exploration of configuration space [82].

Classification and Comparative Analysis of Enhanced Sampling Methods

Enhanced sampling methods encompass a diverse set of approaches that can be broadly categorized into temperature-based, collective variable-based, and history-dependent methods [82] [77] [65].

Table 3: Comparative Analysis of Enhanced Sampling Methods

Method	Working Principle	System Size Suitability	Advantages	Disadvantages	Typical Applications
Replica-Exchange MD (REMD)	Parallel simulations at different temperatures with state exchanges [77] [65]	Small to medium [65]	Broad applicability; parallelizable	High computational cost; temperature range sensitivity [65]	Protein folding; peptide conformation [77] [65]
Metadynamics	"Fills" free energy wells with computational bias [65]	Small to medium [65]	Explores unknown free energy surfaces	Collective variable choice critical [65]	Ligand binding; conformational changes [65]
Simulated Annealing	Gradual temperature decrease during simulation [77]	All sizes [65]	Global minimum search; simple implementation	Non-equilibrium method [77]	Structure prediction; flexible systems [77] [65]
Generalized Simulated Annealing (GSA)	Generalized statistical approach to annealing [77]	Large systems [65]	Low computational cost for large systems	Less common implementation	Large macromolecular complexes [77] [65]
Adaptive Biasing Force (ABF)	Directly applies bias to force along collective variables [65]	Small to medium	Efficient convergence	Requires predefined collective variables	Barrier crossing; conformational transitions [65]

Implementation Protocols for Enhanced Sampling

Replica-Exchange Molecular Dynamics (REMD): This method employs multiple parallel simulations (replicas) at different temperatures, with periodic exchange attempts between neighboring temperatures based on a Metropolis criterion [77] [65]. The probability of exchanging states between two replicas at temperatures Ti and Tj is given by:

[P = \min\left(1, \exp\left(\left(\frac{1}{kB Ti} - \frac{1}{kB Tj}\right)(Ei - Ej)\right)\right)]

where Ei and Ej are the potential energies of the two replicas [77]. REMD efficiency depends critically on proper temperature spacing to maintain adequate exchange rates (typically 20-30%) [65].

Metadynamics: This method enhances sampling by adding a history-dependent bias potential to discourage the system from revisiting previously explored configurations [65]. The bias is constructed as a sum of Gaussian functions deposited along trajectory in collective variable space:

[V(s,t) = \sum{t'= \tauG, 2\tau_G, ...} w \exp\left(-\frac{|s-s(t')|^2}{2\sigma^2}\right)]

where s represents collective variables, τ_G is the deposition stride, w is the Gaussian height, and σ determines Gaussian width [65]. Metadynamics requires careful selection of collective variables that describe the slow degrees of freedom relevant to the process being studied [65].

Simulated Annealing: Inspired by metallurgical annealing, this method employs an artificial temperature schedule that gradually decreases during simulation [77]. Variants include Classical Simulated Annealing (CSA), Fast Simulated Annealing (FSA), and Generalized Simulated Annealing (GSA), with GSA being particularly effective for large macromolecular complexes due to its relatively low computational cost [77] [65].

Integrated Protocols for Molecular Dynamics Simulations

Comprehensive Workflow for Biomolecular Simulations

The following diagram illustrates an integrated protocol incorporating thermostat, barostat, and enhanced sampling methods for comprehensive biomolecular simulation:

Diagram 1: Integrated MD Protocol Workflow. This workflow illustrates the sequential stages of a comprehensive molecular dynamics simulation protocol, highlighting appropriate algorithm selection at each stage.

Specialized Protocol for Drug Target Studies

For studies focused on drug discovery, particularly inhibitor binding to protein targets, the following specialized protocol is recommended:

• System Preparation:

  • Obtain protein structure from PDB or homology modeling
  • Add missing hydrogen atoms and perform protonation states adjustment at physiological pH
  • Solvate the system in an appropriate water model (TIP3P, TIP4P) with ion concentration matching physiological conditions

• Equilibration Phase:

  • Energy Minimization: 5,000-10,000 steps of steepest descent to remove steric clashes
  • NVT Equilibration: 100 ps with Berendsen thermostat (Ï„ = 0.1 ps) and heavy atom position restraints (force constant 1000 kJ/mol/nm²)
  • NPT Equilibration: 100 ps with Berendsen thermostat (Ï„ = 0.1 ps) and Berendsen barostat (Ï„ = 1.0 ps) with same position restraints
  • Unrestrained NPT: 1-5 ns with Berendsen controls until energy and density stabilization

• Enhanced Sampling Phase:

  • For binding site exploration: Well-tempered metadynamics with collective variables describing pocket volume and shape
  • For full conformational sampling: REMD with 24-64 replicas spanning 300-500 K
  • For binding free energy calculations: Adaptive sampling methods focusing on ligand displacement coordinates

• Production Phase:

  • Extended simulation (100 ns - 1 μs) using Nosé-Hoover thermostat (Ï„ = 0.5-1.0 ps) and Parrinello-Rahman barostat (Ï„ = 2.0-5.0 ps)
  • Multiple independent replicates if enhanced sampling not employed

• Analysis:

  • Root-mean-square deviation and fluctuation calculations
  • Principal component analysis for essential dynamics
  • Cluster analysis to identify dominant conformations
  • Free energy calculations from enhanced sampling data

The Scientist's Toolkit: Essential Research Reagents and Computational Tools

Table 4: Essential Research Tools for Molecular Dynamics Simulations

Tool Category	Specific Tools	Function	Application Context
MD Software Packages	GROMACS, NAMD, AMBER [56] [54]	Core simulation engines	All-atom MD simulations with various force fields
Thermostat Algorithms	Berendsen, Nosé-Hoover, Langevin [78]	Temperature regulation	Maintaining constant temperature ensembles
Barostat Algorithms	Berendsen, Parrinello-Rahman, MTTK [80]	Pressure regulation	Maintaining constant pressure ensembles
Enhanced Sampling Methods	REMD, Metadynamics, Simulated Annealing [77] [65]	Accelerate configuration space exploration	Overcoming energy barriers; studying rare events
Force Fields	CHARMM, AMBER, OPLS [56]	Molecular mechanical parameterization	Determining energy and forces between atoms
Analysis Tools	Bio3d, VMD, XPLOR [54]	Trajectory analysis and visualization	Extracting physicochemical insights from simulation data
Specialized Methods	Generalized Simulated Annealing [77]	Global optimization for large systems	Studying large macromolecular complexes like cellulosomes

The strategic selection and implementation of thermostats, barostats, and enhanced sampling methods are critical components of effective molecular dynamics protocols in drug development research. Thermostats and barostats maintain physiological relevance by regulating temperature and pressure, while enhanced sampling methods address the fundamental challenge of inadequate conformational sampling in complex biomolecular systems.

This comparative analysis reveals that algorithm selection must be guided by the specific research question and simulation stage. The Berendsen methods excel in equilibration phases despite their ensemble limitations, while Nosé-Hoover and Parrinello-Rahman methods provide superior ensemble fidelity for production simulations. For enhanced sampling, REMD offers broad applicability for small to medium systems, while metadynamics enables focused exploration of specific conformational transitions, and simulated annealing methods remain valuable for studying large macromolecular complexes.

Future developments in this field will likely focus on increased integration of machine learning and deep learning technologies to further accelerate sampling and improve force field accuracy [56]. Additionally, methodological advances that bridge timescales between molecular dynamics and biological function will enhance the relevance of simulations to drug discovery applications. By thoughtfully combining these algorithmic approaches within integrated protocols, researchers can maximize the biological insights gained from molecular dynamics simulations while maintaining computational efficiency.

Molecular dynamics (MD) simulation is a powerful computational tool for modeling various physicochemical properties, particularly solubility, by providing a detailed perspective on molecular interactions and dynamics [83]. The integration of machine learning (ML) with MD simulations is transforming the landscape of computational chemistry and drug discovery. ML techniques have become powerful tools in both industrial and academic settings due to their ability to facilitate analysis of complex data and generate predictive insights from MD trajectory data [84]. This application note details protocols for leveraging ML in the validation of MD simulations, specifically for automated trajectory analysis and molecular property prediction, framed within the context of drug discovery applications.

Machine Learning Approaches for MD Trajectory Analysis

Core ML Algorithms for Trajectory Analysis

ML methods provide significant utility when parsing through very large MD datasets, particularly for drawing conclusions from methodologies such as MD simulations which result in gigabytes (or more) of atomistic coordinate data [84]. Multiple supervised ML techniques can be implemented to extract meaningful insights from MD trajectories.

Table 1: Machine Learning Algorithms for MD Trajectory Analysis

Algorithm	Key Characteristics	Application in MD Analysis
Logistic Regression	Generalized linear model producing categorical outputs; uses sigmoid function for probability estimation	Determining residue importance for distinguishing between protein variants [84]
Random Forest (RF)	Ensemble of decision trees; uses bootstrap aggregating to reduce variance	Identifying residues most important to differential binding affinities [84]
Multilayer Perceptron (MLP)	Neural network with input nodes, hidden layers, and output layers; enables nonlinear responses	Advanced structural classifications using MD data [84]
Gradient Boosting	Ensemble method building sequential trees to correct previous errors	Predicting aqueous solubility from MD-derived properties [83]

Application Case: Analysis of SARS-CoV-2 Spike Protein

A practical implementation of ML for MD analysis involves studying the SARS-CoV-2 spike protein receptor binding domain (RBD) interacting with the ACE2 receptor [84]. The protocol involves developing a pipeline for processing MD simulation trajectory data and identifying residues that significantly impact the stability of the complex using ML algorithms.

Figure 1. ML workflow for analyzing MD trajectories of viral spike proteins.

ML-Driven Property Prediction from MD Simulations

Key MD-Derived Properties for Solubility Prediction

Through rigorous analysis, researchers have identified specific MD-derived properties with significant influence on aqueous solubility. A study examining 211 drugs from diverse classes identified seven key properties that are highly effective in predicting solubility [83].

Table 2: Key MD-Derived Properties for Solubility Prediction

Property	Description	Influence on Solubility
logP	Octanol-water partition coefficient	Well-established experimental descriptor with significant influence [83]
SASA	Solvent Accessible Surface Area	Represents molecular exposure to solvent environment [83]
Coulombic_t	Coulombic interaction energy	Measures electrostatic interactions with solvent [83]
LJ	Lennard-Jones interaction energy	Quantifies van der Waals interactions [83]
DGSolv	Estimated Solvation Free Energy	Measures energy change during solvation process [83]
RMSD	Root Mean Square Deviation	Indicates structural stability and conformational changes [83]
AvgShell	Average solvents in Solvation Shell	Describes local solvent organization around solute [83]

Ensemble ML Models for Property Prediction

Ensemble machine learning algorithms have demonstrated exceptional performance in predicting molecular properties from MD-derived features. The Gradient Boosting algorithm has achieved the best performance with a predictive R² of 0.87 and an RMSE of 0.537 in test sets for solubility prediction [83].

Figure 2. Property prediction workflow from MD simulations using ensemble ML.

Experimental Protocols

Protocol: MD Simulation Setup for Solubility Prediction

Objective: Generate MD trajectory data for ML-based solubility prediction Materials: GROMACS 5.1.1 software package, GROMOS 54a7 force field [83]

• System Preparation: Model molecules in neutral conformation using GROMOS 54a7 force field to generate topology and initial coordinate files [83].
• Simulation Box: Set up cubic simulation box with appropriate dimensions (e.g., 4×4×4 nm³) to accommodate solute and solvent molecules [83].
• Ensemble Selection: Conduct simulations in the isothermal-isobaric (NPT) ensemble to maintain constant temperature and pressure [83].
• Solvation: Solvate the solute in explicit water models appropriate for the force field.
• Energy Minimization: Perform energy minimization using steepest descent algorithm until maximum force < 1000 kJ/mol/nm.
• Equilibration: Conduct equilibration in NVT and NPT ensembles for 100-500 ps each.
• Production Run: Execute production MD simulation for sufficient duration (typically 10-100 ns) to capture relevant dynamics.

Protocol: ML Model Training for Property Prediction

Objective: Train ensemble ML models to predict aqueous solubility from MD-derived properties Materials: Python/R with scikit-learn, XGBoost libraries; dataset of 211 drugs with experimental solubility values [83]

• Data Collection: Compile dataset of experimental solubility values (logS) ranging from -5.82 to 0.54 (mol/L) from literature sources [83].
• Feature Extraction: Extract ten MD-derived properties from trajectories, plus experimental logP values from literature [83].
• Data Splitting: Randomly split data into training (50%) and internal validation (50%) datasets, ensuring representative distribution of solubility values [83].
• Feature Selection: Apply statistical analysis and feature selection methods to identify the seven most influential properties [83].
• Model Training: Implement four ensemble algorithms: Random Forest, Extra Trees, XGBoost, and Gradient Boosting using selected features [83].
• Hyperparameter Tuning: Optimize model parameters using grid search or Bayesian optimization with cross-validation.
• Model Evaluation: Assess performance using R², RMSE, and other relevant metrics on test set.

Performance Metrics and Validation

The performance of ML models for property prediction should be rigorously validated using multiple metrics:

Table 3: Performance Comparison of Ensemble ML Algorithms for Solubility Prediction

Algorithm	R² Score	RMSE	Key Advantages
Gradient Boosting	0.87	0.537	Highest predictive accuracy [83]
Random Forest	0.85	0.562	Robust to overfitting [83]
XGBoost	0.86	0.551	Computational efficiency [83]
Extra Trees	0.84	0.571	Reduced variance [83]

Research Reagent Solutions

Table 4: Essential Computational Tools for ML-MD Integration

Tool/Category	Specific Examples	Function/Application
MD Software	GROMACS 5.1.1 [83], NAMD [84]	Molecular dynamics simulation engines for trajectory generation
Force Fields	GROMOS 54a7 [83]	Molecular mechanical parameter sets for simulating biomolecules
ML Libraries	scikit-learn, XGBoost [83]	Python libraries implementing ensemble ML algorithms
Analysis Tools	MDTraj, MDAnalysis	Specialized tools for extracting features from MD trajectories
Visualization	VMD, PyMOL	Molecular visualization and analysis of simulation results

The integration of machine learning with molecular dynamics simulations represents a paradigm shift in computational chemistry and drug discovery. The protocols outlined in this application note demonstrate that ML algorithms can effectively analyze complex MD trajectory data and predict critical molecular properties such as solubility with high accuracy [83]. Ensemble methods like Gradient Boosting and Random Forest have shown particular promise, achieving high predictive performance for aqueous solubility using seven key MD-derived properties [83]. As AI and ML technologies continue to evolve, their integration with MD simulations is poised to further accelerate drug discovery pipelines, enhance prediction accuracy, and reduce resource consumption in pharmaceutical development.

This application note provides a comparative evaluation of protein folding algorithms rooted in Molecular Dynamics (MD) simulations. MD simulations serve as a critical in silico microscope, capturing atomic-level behavior and folding pathways by numerically solving Newton's equations of motion for all atoms in a system. We detail standardized protocols for implementing MD-based folding simulations and benchmark these against emerging quantum-classical hybrid algorithms. The performance is quantified using metrics such as root-mean-square deviation (RMSD), energy convergence, and agreement with experimental folding times. This structured analysis aims to guide researchers in selecting and deploying appropriate computational strategies for elucidating protein folding mechanisms and energetics.

Protein folding, the process by which a polypeptide chain attains its native three-dimensional structure, is a fundamental problem in molecular biology with profound implications for understanding cellular function and drug development. Molecular Dynamics (MD) simulation has emerged as a powerful tool for studying this process, predicting how every atom in a protein will move over time based on a general model of the physics governing interatomic interactions [1]. These simulations capture behavior in full atomic detail and at fine temporal resolution, revealing mechanisms of conformational change, ligand binding, and folding [1]. The core principle involves calculating the force on each atom using a molecular mechanics force field and using Newton’s laws of motion to update atomic positions and velocities, resulting in a trajectory that describes the system's atomic-level configuration [1]. This case study frames the evaluation of MD and related algorithms within the broader context of molecular dynamics simulation protocol research, providing a practical framework for scientists.

Featured Folding Algorithms and Methodologies

A diverse set of computational algorithms can be employed within or alongside the MD framework to simulate and analyze protein folding. The following table summarizes the key methodologies evaluated in this case study.

Table 1: Key Protein Folding Algorithms and Methodologies

Algorithm/Method	Core Principle	Key Application in Folding	Notable Implementation
Classical MD [1]	Numerical integration of Newton's equations of motion for all atoms using an empirical force field.	Simulating folding pathways and dynamics from unfolded or partially folded states.	GROMACS [24], AMBER, NAMD
Essential Dynamics Sampling (EDS) [85]	An MD simulation biased to explore configurations along collective motions defined by principal components from an equilibrated trajectory.	Driving folding by reducing the distance to a target native structure in a subspace of essential degrees of freedom.	Custom GROMACS protocols [85]
Targeted MD [85]	Application of time-dependent harmonic restraints to continuously decrease the RMSD of all atoms from a target native structure.	Forcing a direct pathway between unfolded and folded states.	Various MD software suites
Distributed Computing MD [86]	Ensemble simulation of tens of thousands of independent, shorter trajectories to statistically map the folding landscape.	Studying folding kinetics and heterogeneous transition states.	Folding@Home [86]
CVaR-VQE (Quantum-Classical) [87]	A hybrid quantum algorithm using a variational quantum eigensolver optimized with Conditional Value at Risk to find the ground-state energy of a peptide lattice model.	Predicting the lowest energy conformation of small peptides; compared against MD results.	Quantum computing simulators/hardware [87]

Workflow for Molecular Dynamics Folding Simulations

A generalized, peer-reviewed protocol for setting up and running a protein folding simulation using GROMACS involves several key stages [24]. The overall workflow is designed to build a realistic system, equilibrate it, and production-run the simulation for analysis.

Figure 1: Generalized MD Simulation Workflow. The process involves system setup (green), simulation and equilibration (red), and final production and analysis (blue).

Detailed Protocol Steps:

• Obtain and Prepare Protein Coordinates: Download the initial protein structure from the RCSB Protein Data Bank. The structure file (protein.pdb) is processed using the pdb2gmx command to generate molecular topology and coordinate files in GROMACS format, while also selecting an appropriate force field (e.g., ffG53A7 is recommended in GROMACS v5.1) [24].

• Define Periodic Boundary Conditions: A simulation box is defined around the protein to avoid edge effects. A cubic box with a minimum of 1.0 nm distance between the protein and the box edge is standard [24].

• Solvate the System: The box is filled with explicit water molecules to mimic a physiological environment using the solvate command. The topology file is automatically updated to include water [24].

• Add Ions to Neutralize: The system's net charge is neutralized by adding counterions (e.g., Na+/Cl-). This requires first generating a pre-processed run input file (grompp) with an energy minimization parameter file (em.mdp), then using genion [24].

• Energy Minimization: The system is energy-minimized using steepest descent or conjugate gradient methods to remove any steric clashes and produce a relaxed starting configuration [24].

• System Equilibration: The system is equilibrated in two phases: first under an NVT ensemble (constant Number of particles, Volume, and Temperature) for ~100 ps to stabilize the temperature, followed by an NPT ensemble (constant Number of particles, Pressure, and Temperature) for ~100 ps to stabilize the density.

• Production Simulation: A long, unconstrained MD simulation is run, typically for nanoseconds to microseconds, depending on the protein and computing resources. This trajectory is used for analysis.

• Trajectory Analysis: The resulting trajectory files are analyzed for properties such as RMSD, radius of gyration (Rg), secondary structure evolution, and free energy landscapes.

Advanced and Complementary Algorithms

Essential Dynamics Sampling (EDS): This technique biases an MD simulation to explore configurations along collective motions defined by a principal component analysis of an equilibrated trajectory. In a folding context, a "contraction procedure" accepts only MD steps that do not increase the distance from the target native structure in a chosen subspace of essential eigenvectors. This method has been successfully applied to fold cytochrome c starting from highly unfolded states (RMSD ~20 Ã…) [85].

Distributed Computing and Folding@Home: This approach leverages a massive number of independent, shorter simulations (e.g., tens of thousands of 5–20 ns trajectories) to map the folding landscape statistically. This allows for the study of folding as a heterogeneous reaction involving an ensemble of transition states. Studies on the BBA5 mini-protein have shown excellent agreement between such simulations and laser temperature-jump experiments for mean folding times and equilibrium constants [86].

Quantum-CLASSICAL HYBRID (CVaR-VQE): This algorithm uses a variational quantum eigensolver (VQE) to compute the energy of a peptide lattice model. The VQE is optimized using a Conditional Value at Risk (CVaR) over many iterations to find the least ground-state energy value, which corresponds to the folded conformation. A recent study used this to predict the lowest energy value for 50 peptides and reported more efficient folding outcomes compared to MD simulations and structural alphabet analysis [87].

Comparative Performance Evaluation

The performance of different MD-based approaches can be quantitatively evaluated by comparing their computational demands, timescales, and accuracy against experimental data.

Table 2: Comparative Performance of Folding Simulation Approaches

Simulation Approach	Typical System Size	Accessible Timescale	Key Performance Metric	Reported Result Example
Classical MD (GPUs) [1]	10,000 - 100,000 atoms	Nanoseconds to microseconds	Folding time, RMSD to native	Microsecond folding for fast-folding proteins [86]
Distributed Computing MD [86]	Small proteins (~50 atoms)	Statistically equivalent to µs-ms	Mean folding time, equilibrium constant	Excellent agreement with laser T-jump experiments for BBA5 [86]
Essential Dynamics Sampling [85]	Cytochrome c (104 AA)	Efficiently reaches native state	RMSD from native, pathway agreement	Correct folding from 20 Ã… RMSD starting structure [85]
CVaR-VQE (Quantum) [87]	7-amino acid peptides	N/A (Energy minimization)	Ground-state energy value	Efficient folding vs. 50 ns MD simulations [87]

The Scientist's Toolkit: Research Reagent Solutions

The following table details essential software, tools, and "reagents" required to perform MD simulations for protein folding.

Table 3: Essential Research Reagents and Software Solutions

Item	Specification/Function	Example & Notes
MD Simulation Suite	Software for performing all stages of simulation.	GROMACS [24], AMBER, NAMD, CHARMM. GROMACS is open-source and highly optimized.
Molecular Visualization	Tool for visual inspection of structures and trajectories.	RasMol [24], VMD, PyMOL.
Force Field	Empirical potential energy function defining interatomic interactions.	GROMOS [85], OPLS [87], AMBER, CHARMM. Choice impacts accuracy.
Water Model	Explicit solvent model to mimic aqueous environment.	SPC, SPC/E, TIP3P, TIP4P [87]. TIP3P is common.
Parameter File (.mdp)	Defines simulation parameters for each step (minimization, equilibration, production).	Obtained from software manual/tutorials; critical for control [24].
High-Performance Computing	Parallel computing resources (CPU/GPU clusters).	Required for production runs; local workstations can handle setup [24].

This case study demonstrates that Molecular Dynamics provides a versatile and powerful framework for simulating protein folding, with several specialized algorithms available for different research questions. Classical MD with modern hardware offers direct observation of folding pathways, while methods like EDS can efficiently guide folding using prior knowledge. Ensemble approaches using distributed computing excel at reproducing experimental kinetics. Emerging hybrid quantum-classical algorithms show promise for predicting ground-state energies of small peptides. The provided protocols and comparisons offer a foundation for researchers to implement these methods, contributing to advancements in structural biology, understanding of disease mechanisms, and structure-based drug design.

Conclusion

Molecular dynamics simulation has evolved into an indispensable tool that provides atomic-level insight into biological and chemical processes, directly impacting drug discovery and materials science. The key to its successful application lies in a rigorous, multi-stage process: a robust foundational setup, the selection of advanced methods tailored to the biological question, proactive troubleshooting to ensure stability and sampling, and, crucially, rigorous validation against experimental data. Future directions point toward an even tighter integration of machine learning to create more accurate and efficient potentials, guide sampling, and analyze complex datasets. Furthermore, the development of multiscale models that seamlessly combine quantum, atomic, and coarse-grained descriptions will be critical for simulating large, complex systems like cellular environments. These advancements, coupled with growing computational power, will solidify MD's role as a predictive pillar in biomedical and clinical research, accelerating the design of novel therapeutics and materials.

References

• 1. Molecular dynamics simulation for all - PMC - PubMed Central [https://pmc.ncbi.nlm.nih.gov/articles/PMC6209097/]
• 2. Force field (chemistry) [https://en.wikipedia.org/wiki/Force_field_(chemistry)]
• 3. Data scheme and data format for transferable force fields ... [https://www.nature.com/articles/s41597-023-02369-8]
• 4. Force Fields and Interactions - GitHub Pages [https://computecanada.github.io/molmodsim-md-theory-lesson-novice/01-Force_Fields_and_Interactions/index.html]
• 5. Current Status of Protein Force Fields for Molecular ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4554537/]
• 6. Martini Force Field Initiative [https://cgmartini.nl/]
• 7. Leveraging high-throughput molecular simulations and ... [https://www.nature.com/articles/s41524-025-01552-2]
• 8. Data-driven parametrization of molecular mechanics force ... [https://pubs.rsc.org/en/content/articlehtml/2025/sc/d4sc06640e]
• 9. 2.6. Molecular Dynamics (MD) Simulation [https://bio-protocol.org/exchange/minidetail?id=6660704&type=30]
• 10. Molecular dynamics simulations: advances and applications [https://pmc.ncbi.nlm.nih.gov/articles/PMC4655909/]
• 11. Checking and Preparing PDB Files [https://computecanada.github.io/molmodsim-amber-md-lesson/10-Checking_PDB_Files/index.html]
• 12. Molecular Dynamics - GROMACS 2025.3 documentation [https://manual.gromacs.org/documentation/current/reference-manual/algorithms/molecular-dynamics.html]
• 13. About GROMACS [https://www.gromacs.org/about.html]
• 14. GROMACS [https://en.wikipedia.org/wiki/GROMACS]
• 15. Comparison of software for molecular mechanics modeling [https://en.wikipedia.org/wiki/Comparison_of_software_for_molecular_mechanics_modeling]
• 16. Molecular Dynamics - SCM [https://www.scm.com/tools/molecular-dynamics/]
• 17. Amsterdam Modeling Suite - SCM [https://www.scm.com/amsterdam-modeling-suite/]
• 18. Best CPU, GPU, RAM for Molecular Dynamics in 2024 ... [https://bizon-tech.com/blog/best-cpu-gpu-ram-for-molecular-dynamics?srsltid=AfmBOorbFyi5aDL1FlhuwTBbO-Z4JW3HW0OkZFg1CoLEyu692QC_qP66]
• 19. How Well Do Molecular Dynamics Force Fields Model ... [https://pubmed.ncbi.nlm.nih.gov/40766644/]
• 20. Running Molecular Dynamics on Alliance clusters with AMBER [https://computecanada.github.io/molmodsim-amber-md-lesson/26-MD_Software_Benchmarks/index.html]
• 21. Periodic boundary conditions [https://manual.gromacs.org/2025.1/reference-manual/algorithms/periodic-boundary-conditions.html]
• 22. Wrapping tutorial or “why is my simulation exploding?” [https://software.acellera.com/htmd/tutorials/WrappingTutorial.html]
• 23. Explicit Solvent Molecular Dynamics (MD) Simulations. [https://bio-protocol.org/exchange/minidetail?id=18115607&type=30]
• 24. Protocol for Molecular Dynamics Simulations of Proteins [https://en.bio-protocol.org/en/bpdetail?id=2051&type=0]
• 25. Molecular Dynamics Simulations of RNA Stem-Loop Folding ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12593105/]
• 26. for Protocol of Proteins Molecular Dynamics Simulations [https://bio-protocol.org/en/bpdetail?id=2051&type=0]
• 27. for Protocols of RNA Nanostructures Molecular Dynamics Simulations [https://experiments.springernature.com/articles/10.1007/978-1-4939-7138-1_3?error=cookies_not_supported&code=1beea1bd-19d5-4baf-9e98-3f253418d201]
• 28. Uncertainty in MD-Derived Diffusion Coefficients Depends on Analysis... [https://chemrxiv.org/engage/chemrxiv/article-details/69171ab6a10c9f5ca15bda41]
• 29. Best CPU, GPU, RAM for Molecular Dynamics in 2024 ... [https://bizon-tech.com/blog/best-cpu-gpu-ram-for-molecular-dynamics?srsltid=AfmBOop6Pg-cKI8A_WkYdgYagWh6jfsWvhrVilxtbkgqdLtkAgchUXsh]
• 30. Scientific modeling on cloud GPUs: fit guide for 2025 [https://compute.hivenet.com/post/scientific-modeling-cloud-gpus-fit-guide]
• 31. Welcome to GROMACS — GROMACS webpage https://www ... [https://www.gromacs.org/]
• 32. LAMMPS Molecular Dynamics Simulator [https://www.lammps.org/]
• 33. Enabling Scalable AI-Driven Molecular Dynamics ... [https://developer.nvidia.com/blog/enabling-scalable-ai-driven-molecular-dynamics-simulations/]
• 34. A multiscale simulation approach to compute protein ... [https://chemrxiv.org/engage/chemrxiv/article-details/685a5ad83ba0887c3347dc85]
• 35. Rowan | ML-Powered Molecular Design and Simulation [https://www.rowansci.com/]
• 36. Challenges and opportunities in computational studies for ... [https://www.nature.com/articles/s44386-025-00024-3]
• 37. Molecular Dynamics Simulation of Lipid Nanoparticles ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11433737/]
• 38. In vivo demonstration of enhanced mRNA delivery by cyclic ... [https://pubs.rsc.org/en/content/articlehtml/2025/md/d5md00084j]
• 39. Lipid polymer hybrid nanoparticles: a custom-tailored next ... [https://molecular-cancer.biomedcentral.com/articles/10.1186/s12943-023-01849-0]
• 40. New Applications of Lipid and Polymer-Based Nanoparticles ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8708541/]
• 41. Enhancing nucleic acid delivery by the integration of ... [https://www.frontiersin.org/journals/medical-technology/articles/10.3389/fmedt.2025.1591119/full]
• 42. Hamiltonian replica exchange augmented with diffusion ... [https://arxiv.org/html/2505.08357v2]
• 43. Replica exchange of expanded ensembles: A generalized ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11740319/]
• 44. Replica exchange - GROMACS 2025-rc documentation [https://manual.gromacs.org/documentation/2025-rc/reference-manual/algorithms/replica-exchange.html]
• 45. PySAGES: flexible, advanced sampling methods ... [https://www.nature.com/articles/s41524-023-01189-z]
• 46. Combining stochastic resetting with Metadynamics to ... [https://www.nature.com/articles/s41467-023-44528-w]
• 47. Molecular Dynamics Simulations in Drug Discovery and ... [https://www.mdpi.com/2227-9717/9/1/71]
• 48. Multiscale simulation approaches to modeling drug– ... [https://www.sciencedirect.com/science/article/abs/pii/S0959440X20300142]
• 49. Comparison Between All-Atom and Coarse-Grained ... [https://global-sci.com/index.php/cicc/article/view/22829]
• 50. A Practical Guide to All-Atom and Coarse-Grained ... [https://www.mdpi.com/1422-0067/25/12/6698]
• 51. Multiscale Modeling in the Clinic: Drug Design and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4983472/]
• 52. Model-Informed Drug Development Paired Meeting Program [https://www.fda.gov/drugs/development-resources/model-informed-drug-development-paired-meeting-program]
• 53. Molecular dynamics parameters (.mdp options) [https://manual.gromacs.org/current/user-guide/mdp-options.html]
• 54. Novel procedure for thermal equilibration in molecular ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4128190/]
• 55. A molecular dynamics simulation study on hydrocarbon ... [https://pubs.rsc.org/en/content/articlehtml/2025/cp/d4cp04588b]
• 56. Molecular dynamics simulations of proteins: an in-depth ... [https://pubmed.ncbi.nlm.nih.gov/41003729/]
• 57. Best CPU, GPU, RAM for Molecular Dynamics in 2024 ... [https://bizon-tech.com/blog/best-cpu-gpu-ram-for-molecular-dynamics?srsltid=AfmBOookamuyTzKeLCYjbPUnTli9aeLzlXIz_gGQSt8vNtoeIlwYGnWx]
• 58. A review of molecular dynamic simulation on polymer ... [https://www.sciencedirect.com/science/article/pii/S0378775325019792]
• 59. Frontier advances in molecular dynamics simulations for the ... [https://pubs.rsc.org/en/content/articlehtml/2025/ra/d5ra00059a?page=search]
• 60. Molecular dynamics — AMS 2025.1 documentation - SCM [https://www.scm.com/doc/AMS/Tasks/Molecular_Dynamics.html]
• 61. Parallelization - GROMACS 2025.1 documentation [https://manual.gromacs.org/documentation/2025.1/reference-manual/algorithms/parallelization-domain-decomp.html]
• 62. Learning the action for long-time-step simulations of ... [https://arxiv.org/html/2508.01068v1]
• 63. Getting good performance from mdrun [https://manual.gromacs.org/documentation/2025.2/user-guide/mdrun-performance.html]
• 64. Parallelization (MPI and OpenMP) - SCM [https://www.scm.com/doc/ReaxFF/Parallelization.html]
• 65. Enhanced Sampling Techniques in Molecular Dynamics ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4339458/]
• 66. Enhanced sampling of protein conformational changes via ... [https://www.nature.com/articles/s41467-025-55983-y]
• 67. Machine learning heralding a new development phase in ... [https://link.springer.com/article/10.1007/s10462-024-10731-4]
• 68. A Standardized Benchmark for Machine-Learned ... [https://arxiv.org/html/2510.17187v1]
• 69. Automated sampling assessment for molecular simulations ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3017371/]
• 70. Modeling the potential energy surface by force fields for ... [https://pubs.rsc.org/en/content/articlehtml/2025/sc/d5sc02715b?page=search]
• 71. Force Field Limitations of All-Atom Continuous Constant ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12231151/]
• 72. From byte to bench to bedside: molecular dynamics ... [https://bmcbiol.biomedcentral.com/articles/10.1186/s12915-023-01791-z]
• 73. Structure and dynamics in drug discovery [https://www.nature.com/articles/s44386-024-00001-2]
• 74. AQuaRef: machine learning accelerated quantum ... [https://www.nature.com/articles/s41467-025-64313-1]
• 75. Validating Molecular Dynamics Simulations Against ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6420231/]
• 76. A beginner's guide to molecular dynamics simulations and ... [https://www.sciencedirect.com/science/article/abs/pii/S0076687920301488]
• 77. Enhanced sampling techniques in molecular dynamics ... [https://www.sciencedirect.com/science/article/abs/pii/S0304416514003559]
• 78. Controlling Temperature - GitHub Pages [https://computecanada.github.io/molmodsim-md-theory-lesson-novice/07-thermostats/index.html]
• 79. Molecular Dynamics - Temperature [https://www.uoxray.uoregon.edu/local/manuals/biosym/discovery/General/Dynamics/Temperature.html]
• 80. Controlling Pressure – Practical considerations for Molecular ... [https://computecanada.github.io/molmodsim-md-theory-lesson-novice/08-barostats/index.html]
• 81. Pressure-controlled molecular dynamics study on the ... [https://www.sciencedirect.com/science/article/abs/pii/S1359431125021301]
• 82. Enhanced sampling methods for molecular dynamics ... [https://arxiv.org/abs/2202.04164]
• 83. Machine learning analysis of molecular dynamics ... [https://www.nature.com/articles/s41598-025-11392-1]
• 84. Using Machine Learning to Analyze Molecular Dynamics ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12147208/]
• 85. Molecular Dynamics Simulation of Protein Folding by ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC1303567/]
• 86. Absolute comparison of simulated and experimental protein - folding ... [https://www.nature.com/articles/nature01160?error=cookies_not_supported&code=ff34d78b-6cc2-4869-a21f-fff50e40d1d2]
• 87. A comparative insight into peptide folding with quantum CVaR-VQE... [https://link.springer.com/article/10.1007/s11128-024-04261-9]